Ytukyg

Physikalische Einheit
Einheitenname	Astronomische Einheit
Einheitenzeichen	AE,AU,au,ua{displaystyle mathrm {AE,AU,au,ua} }
Physikalische Größe(n)	Länge
Formelzeichen	l{displaystyle l}
Dimension	L{displaystyle {mathsf {L}}}
System	Zum Gebrauch mit dem SI zugelassen
In SI-Einheiten	1AE=149.597.870.700m{displaystyle mathrm {1,AE=149.597.870.700;m} } (exakt)
Abgeleitet von	Erdbahnradius

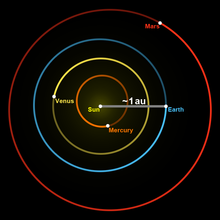
Veranschaulichung der Astronomischen Einheit (englisch au), grau

Die Astronomische Einheit (abgekürzt AE, international au für englisch astronomical unit) ist ein Längenmaß in der Astronomie: Laut Definition misst eine AE exakt 149 597 870 700 Meter. Das ist ungefähr der mittlere Abstand zwischen Erde und Sonne.

Die Astronomische Einheit ist neben dem Lichtjahr und dem Parsec die wichtigste Einheit unter den astronomischen Maßeinheiten. Sie gehört nicht zum Internationalen Einheitensystem (SI), ist aber zum Gebrauch mit dem SI zugelassen.^[1] Sie ist keine gesetzliche Maßeinheit.^[2]

Die Astronomische Einheit war historisch von großer Bedeutung für die Astronomie, da die meisten Entfernungsbestimmungen aufgrund der verwendeten Methoden das Ergebnis unmittelbar in AE und nicht in Metern lieferten. Mittlerweile ist jedoch der Umrechenfaktor zwischen AE und Metern so genau bekannt, dass die Verwendung der AE keine Genauigkeitsvorteile mehr bietet. Im Jahre 2012 wurde daher die frühere, von der Gravitationskonstante der Sonne abgeleitete Definition aufgegeben und die AE einfach als eine bestimmte Anzahl von Metern neu definiert. Damit hat die AE ihre ursprüngliche astrophysikalische Bedeutung verloren und ist nur noch eine konventionelle Längeneinheit. Entfernungen innerhalb des Sonnensystems werden jedoch immer noch meist in AE angegeben, da sich so bequeme Zahlenwerte ergeben.

Das Internationale Büro für Maß und Gewicht empfiehlt seit 2014 ^[3] für die Astronomische Einheit ebenso wie die Internationale Astronomische Union (IAU) das Einheitenzeichen au.^[4] Im Gegensatz dazu hat sich in der deutschsprachigen Literatur die Verwendung von AE und AU durchgesetzt.

Ausgedrückt in anderen interstellaren Längenmaßen ergibt sich für die Astronomische Einheit folgende Größenrelation:

1 AE  =  499,004 784   Lichtsekunden
1 AE  =  1,581 250 74 · 10⁻⁵ Lichtjahre
1 AE  =  4,848 136 81 · 10⁻⁶ Parsec
1 AE  =  2π / (360·60·60) Parsec

Definition |

Die AE war ursprünglich als die Länge der großen Halbachse der Erdbahn definiert, später als Radius einer Kreisbahn, auf der ein hypothetischer masseloser Körper die Sonne in einem vorgegebenen Zeitraum umrundete (nähere Details werden im Abschnitt Geschichte erläutert).

Am 30. August 2012 beschloss die in Peking tagende 28. Generalversammlung der Internationalen Astronomischen Union in „Resolution B2“,^[5]

“… that the astronomical unit be re-defined to be a conventional unit of length equal to 149 597 870 700 m exactly, […]”[4]

„… dass die Astronomische Einheit neu definiert werde als eine konventionelle Längeneinheit, welche exakt 149 597 870 700 m entspricht, […]“

Gemäß dieser Neudefinition ist die AE nun keine durch Messung zu ermittelnde Eigenschaft des Sonnensystems mehr, sondern sie ist eine Strecke mit einer per Definition exakt festgelegten Länge in Metern. Der gewählte Zahlenwert entspricht dem bis dahin besten Messwert^[6] von 149 597 870 700 m ± 3 m.

Die vorherige Definition der AE beruhte auf der Gaußschen Gravitationskonstanten, welche, wenn sie unter Verwendung der Längeneinheit „1 AE“, der Zeiteinheit „1 Tag“ und der Masseneinheit „1 Sonnenmasse“ ausgedrückt wurde, einen per Konvention fix vorgegebenen Zahlenwert hatte (siehe →Abschnitt Definition von 1976). Welchen Zahlenwert die so definierte Längeneinheit „1 AE“ annahm, wenn sie in SI-Einheiten (also in Metern) ausgedrückt werden sollte, musste durch Beobachtung der Planetenbewegungen ermittelt werden. Infolge der Neudefinition ist die Länge der AE in Metern nun festgelegt; die Gaußsche Gravitationskonstante wird nicht mehr benötigt und ist künftig nicht mehr Bestandteil der astronomischen Konstantensysteme.

Der Zahlenwert der in astronomischen Maßeinheiten ausgedrückten Heliozentrischen Gravitationskonstanten GM⊙{displaystyle GM_{odot }} war gemäß der vorherigen Definition als Konstante festgelegt. In die Berechnung ihres Zahlenwertes in SI-Einheiten ging jedoch der jeweils aktuelle durch Beobachtung bestimmte Zahlenwert für die Länge der Astronomischen Einheit ein, so dass eine Neuvermessung der AE ein verändertes GM⊙{displaystyle GM_{odot }} nach sich ziehen konnte. Die aufgrund moderner Messungen möglich gewordene direkte Bestimmung von GM⊙{displaystyle GM_{odot }} in SI-Einheiten macht diesen Umweg über die AE überflüssig. Außerdem ist denkbar, dass eine mögliche zeitliche Änderung von GM⊙{displaystyle GM_{odot }} in absehbarer Zeit in den Bereich der Messbarkeit rücken könnte. Dies hätte nach der vorherigen Definition die Einführung einer zeitlich veränderlichen AE erfordert, was sich nach der neuen Definition aber erübrigt.^[7] Neuere Messungen (2011) deuten bereits eine geringfügige Abnahme^[8] von GM⊙{displaystyle GM_{odot }} an.

Die Genauigkeit moderner Positionsmessungen im Sonnensystem ist so hoch, dass relativistische Korrekturen berücksichtigt werden müssen. Die Übertragung der vorherigen Definition in einen relativistischen Begriffsrahmen hätte zusätzliche Konventionen erfordert und eine vom Bezugssystem abhängige Länge der AE ergeben. Die neu definierte AE hingegen hat in allen relativistischen Bezugssystemen dieselbe Länge.^[5] Die Resolution legt explizit fest, dass dieselbe Definition für alle relativistischen Zeitskalen (z. B. TCB, TDB, TCG, TT usw.) verwendet werden soll.^[4]

Geschichte |

AE als Längeneinheit |

Die Umlaufzeiten der Planeten sind leicht zu beobachten und waren schon frühen Astronomen sehr genau bekannt. Mit Hilfe des Dritten Keplerschen Gesetzes ließ sich aus dem Verhältnis der Umlaufzeiten zweier Planeten mit praktisch derselben Genauigkeit auf das Verhältnis ihrer Bahnradien schließen. Die damaligen Ephemeriden konnten daher mit hoher Genauigkeit berechnen, wievielmal z. B. Mars zu einem gegebenen Zeitpunkt weiter von der Sonne entfernt war als die Erde. Man wählte die große Halbachse der Erdbahn als Längenmaß, nannte sie „Astronomische Einheit“ und konnte anstelle der umständlichen Ausdrucksweise „Mars ist heute 1,438 mal so weit von der Sonne entfernt wie die große Halbachse der Erdbahn lang ist“ gleichbedeutend einfach sagen „Mars ist heute 1,438 AE von der Sonne entfernt“. Die in dieser Form als AE ausgedrückten Entfernungen (eigentlich die Verhältnisse zweier Entfernungen zueinander) waren recht genau bestimmbar, in irdischen Längenmaßen wie z. B. Meilen oder Metern waren die Entfernungen jedoch nur recht ungenau bekannt. Für wissenschaftliche Zwecke bot sich daher die Verwendung der AE als Längeneinheit an, wofür sie jedoch einer hinreichend genauen Definition bedurfte.

Erste Definition |

Gemäß dem Dritten Keplerschen Gesetz gilt für die Umlaufdauer UP{displaystyle U_{P}} eines Planeten der Masse MP{displaystyle M_{P}}, welcher die Sonne (Masse M⊙{displaystyle M_{odot }}) auf einer Bahn mit der großen Halbachse aP{displaystyle a_{P}} umläuft:^[9]

UP2aP3=4π2G⋅(M⊙+MP){displaystyle {frac {U_{mathrm {P} }^{2}}{a_{mathrm {P} }^{3}}}={frac {4,pi ^{2}}{Gcdot (M_{odot }+M_{mathrm {P} })}}}

(1)

Für zwei Planeten P1 und P2 folgt daraus:

UP12UP22⋅M⊙+MP1M⊙+MP2=aP13aP23{displaystyle {frac {U_{mathrm {P1} }^{2}}{U_{mathrm {P2} }^{2}}}cdot {frac {M_{odot }+M_{mathrm {P1} }}{M_{odot }+M_{mathrm {P2} }}}={frac {a_{mathrm {P1} }^{3}}{a_{mathrm {P2} }^{3}}}}

(2)

Dieses Gesetz enthält nur Verhältnisse der Umlaufzeiten, der Massen und der großen Halbachsen. Das Zweite Keplersche Gesetz enthält in ähnlicher Weise nur eine Aussage über die Verhältnisse der vom Fahrstrahl in bestimmten Zeitintervallen überstrichenen Flächen. Diese Gesetze liefern die Positionen der Planeten daher zunächst in einem noch unbestimmten Maßstab. Man kann deshalb die Einheiten der vorkommenden Längen, Zeitintervalle und Massen so wählen, dass sie die Rechnungen möglichst einfach gestalten. In der klassischen Astronomie wählte man üblicherweise als astronomische Längeneinheit die Länge der großen Halbachse der Erdbahn (1 AE), als astronomische Masseneinheit die Masse der Sonne 1 M_☉ und als astronomische Zeiteinheit den Tag 1 d.

Da die Positionen der Himmelskörper an der scheinbaren Himmelskugel (also die Richtungswinkel, unter denen sie dem Beobachter erscheinen) von absoluten Maßstäben unabhängig sind, konnten die Astronomen mit diesen relativen Maßstäben bereits hochpräzise Positionsastronomie betreiben. Die Entfernung eines Planeten konnte außerdem für einen gewünschten Zeitpunkt mit hoher Genauigkeit in Astronomischen Einheiten angegeben werden, die Entfernung in Metern hingegen weit weniger genau, da die Länge der Astronomischen Einheit in Metern nur mäßig genau bekannt war. Ähnlich konnten die Massen der Planeten recht genau in Sonnenmassen angegeben werden, deutlich weniger genau in Kilogramm.

Erst in den letzten Jahrzehnten wurde es möglich, Entfernungen mit hoher Genauigkeit zu messen (z. B. mittels Laser-Entfernungsmessung zum Mond, mittels Radar-Entfernungsmessung zu Merkur, Venus und Mars, oder mittels Messung der Signallaufzeiten zu Raumsonden).

Gaußsche Gravitationskonstante |

Der Zahlenwert der Gravitationskonstanten G{displaystyle G} in der Gleichung  (1) hängt von der Wahl der Einheiten für die vorkommenden physikalischen Größen ab. Für die Umlaufdauer des Planeten P{displaystyle P} folgt aus jener Gleichung durch Umstellen:

UP=2π⋅aP32G⋅M⊙(1+MPM⊙){displaystyle U_{mathrm {P} }={frac {2pi cdot a_{mathrm {P} }^{frac {3}{2}}}{{sqrt {G}}cdot {sqrt {M_{odot }(1+{frac {M_{mathrm {P} }}{M_{odot }}})}}}}}

(3)

Mit den Abkürzungen

k:=G{displaystyle k:={sqrt {G}}} und μP:=MPM⊙{displaystyle mu _{mathrm {P} }:={frac {M_{mathrm {P} }}{M_{odot }}}}

(4)

ergibt sich:

UP=2π⋅aP32k⋅M⊙(1+μP){displaystyle U_{mathrm {P} }={frac {2pi cdot a_{mathrm {P} }^{frac {3}{2}}}{kcdot {sqrt {M_{odot }(1+mu _{mathrm {P} })}}}}}

(5)

C. F. Gauß bestimmte 1809 den Wert der Gravitationskonstanten k{displaystyle k} in astronomischen Maßeinheiten (große Halbachse der Erdbahn als Längeneinheit AE, mittlerer Sonnentag als Zeiteinheit d, Sonnenmasse als Masseneinheit M⊙{displaystyle M_{odot }}), indem er die Formel auf die Erde E{displaystyle E} als Planet P{displaystyle P} anwandte

aP=aE=1 AE{displaystyle a_{mathrm {P} }=a_{mathrm {E} }=1 mathrm {AE} }

(6)

M⊙=1M⊙{displaystyle M_{odot }=1;mathrm {M_{odot }} }

(7)

und die damals besten Zahlenwerte für UE{displaystyle U_{E}} und μE{displaystyle mu _{E}} einsetzte:^[10]

UP=UE=365,2563835d{displaystyle U_{mathrm {P} }=U_{mathrm {E} }=365{,}2563835;mathrm {d} }

(8)

(siderisches Jahr)

μP=μE=1354710=0,0000028192{displaystyle mu _{mathrm {P} }=mu _{mathrm {E} }={frac {1}{354710}}=0{,}0000028192}

(9)

k=2π⋅aE32UE⋅M⊙(1+μE)=0,01720209895 AE32dM⊙{displaystyle k={frac {2pi cdot a_{mathrm {E} }^{frac {3}{2}}}{U_{mathrm {E} }cdot {sqrt {mathrm {M_{odot }} left(1+mu _{mathrm {E} }right)}}}}=0{,}017,202,098,95 {frac {mathrm {AE} ^{frac {3}{2}}}{mathrm {d} ,{sqrt {mathrm {M_{odot }} }}}}}

(10)

Dieser Zahlenwert der Gravitationskonstanten in astronomischen Maßeinheiten wurde in der Folge als Standardwert für zahlreiche astronomische Berechnungen verwendet.

Definition von 1976 |

Mit stets verbesserter Kenntnis von UE{displaystyle U_{E}} und μE{displaystyle mu _{E}} hätte der Zahlenwert von k{displaystyle k} ständig verbessert werden können. Der gaußsche Wert lag jedoch bald zahlreichen fundamentalen Tabellen zugrunde, welche bei jeder Veränderung von k{displaystyle k} hätten neu berechnet werden müssen.^[11] Eine Alternative bestand darin, in der Gleichung

UE=2π⋅aE32k⋅1+μE{displaystyle U_{mathrm {E} }={frac {2pi cdot a_{mathrm {E} }^{frac {3}{2}}}{kcdot {sqrt {1+mu _{mathrm {E} }}}}}}

(11)

den Zahlenwert von k{displaystyle k} beizubehalten und stattdessen die Längeneinheit, in der aE{displaystyle a_{E}} gemessen wird, so anzupassen, dass der in der neuen Längeneinheit gemessene neue Zahlenwert von aE{displaystyle a_{E}} die Gleichung für die neuen Werte von UE{displaystyle U_{E}} und μE{displaystyle mu _{E}} wieder erfüllt (ein Beispiel folgt im nächsten Abschnitt). Die große Halbachse aE{displaystyle a_{E}} der Erdbahn verlor damit ihren definierenden Status: Sie hatte in astronomischen Maßeinheiten nicht mehr strikt die Länge 1 AE. Die Längeneinheit, bezüglich welcher aE{displaystyle a_{E}} den die Gleichung erfüllenden Zahlenwert annahm, war die neue AE. Damit lautete die Definition von 1976:

Da die Definition der AE damit aber ohnehin nicht mehr unmittelbar durch die Erdbahn gegeben war, lösten sich die Astronomen von der Erdmasse μE{displaystyle mu _{E}} und bezogen die neue Definition auf einen fiktiven Körper f{displaystyle f} mit vernachlässigbar kleiner Masse:

μf→0{displaystyle mu _{mathrm {f} },rightarrow ,0}

(12)

Denkt man sich einen solchen fiktiven Körper auf einer ungestörten Bahn, welche dem Gesetz  (1) gehorcht und deren große Halbachse gleich der zu bestimmenden neuen Längeneinheit ist

af=1AE{displaystyle a_{mathrm {f} }=1,mathrm {AE} }

(13)

so gilt für ihn

Uf=2π⋅132k⋅1+0=2πk{displaystyle U_{mathrm {f} }={frac {2pi cdot 1^{frac {3}{2}}}{kcdot {sqrt {1+0}}}}={frac {2pi }{k}}}

(14)

Dieser definierende Körper hat also eine Umlaufdauer von

2πk=365,256898326…{displaystyle {frac {2pi }{k}}=365{,}256898326dots } Tagen

(15)

(sogen. Gaußsches Jahr)[13]

Die fiktive Bahn lässt sich ohne Beschränkung der Allgemeingültigkeit als kreisförmig annehmen. Die Definition der AE lässt sich daher gleichbedeutend formulieren als

Die Praxis, den Zahlenwert von k{displaystyle k} festzuhalten und durch ihn die AE zu definieren, war inoffiziell seit dem 19. Jahrhundert üblich. Sie wurde 1938 offiziell von der IAU übernommen, als sie auf der 6. Generalversammlung den gaußschen Zahlenwert für k{displaystyle k} per Resolution^[15] festschrieb. 1976 erfolgte auf der 28. Generalversammlung erstmals eine explizite textliche Definition.^[4]

Erdbahn und AE |

Für die Umlaufzeiten der Erde E{displaystyle E} und des definierenden fiktiven Körpers f{displaystyle f} liefert das Dritte Keplergesetz  (2):

UE2Uf2⋅M⊙+MEM⊙+0=aE3af3=aE31AE3{displaystyle {frac {U_{mathrm {E} }^{2}}{U_{mathrm {f} }^{2}}}cdot {frac {M_{odot }+M_{mathrm {E} }}{M_{odot }+0}}={frac {a_{mathrm {E} }^{3}}{a_{mathrm {f} }^{3}}}={frac {a_{mathrm {E} }^{3}}{1,mathrm {AE} ^{3}}}}

(21)

Auflösen nach aE{displaystyle a_{E}} und Einsetzen der aktuellen Zahlenwerte

μE=1328900,561400{displaystyle mu _{mathrm {E} }={frac {1}{328900{,}561400}}} [16]

(22)

und

UE=365,256363d{displaystyle U_{mathrm {E} }=365{,}256363,mathrm {d} } [17]

(23)

ergibt

aE=UE2(2π/k)2⋅(1+μE)3=1,000000036AE{displaystyle a_{mathrm {E} }={sqrt[{3}]{{frac {U_{mathrm {E} }^{2}}{(2pi /k)^{2}}}cdot (1+mu _{mathrm {E} })}}=1{,}000000036,mathrm {AE} } [18]

(24)

Aus dem Verhältnis der Umlaufzeiten beider Körper folgt also das Verhältnis ihrer großen Halbachsen  (21). Die eine davon definiert aber gerade die Astronomische Einheit; das Ergebnis ist also die in AE ausgedrückte große Halbachse der Erdbahn, welche nun etwas größer ist als 1 AE.

Setzt man diese neuen Zahlenwerte für aE{displaystyle a_{E}}, UE{displaystyle U_{E}} und μE{displaystyle mu _{E}} anstelle der alten gaußschen Werte in die gaußsche Formel  (10) ein, so erhält man nach wie vor den gaußschen Zahlenwert für k{displaystyle k}. Wenn der in Tagen gemessenen Umlaufzeit der genannte Zahlenwert UE{displaystyle U_{E}} und der in Sonnenmassen gemessenen Erdmasse der genannte Zahlenwert μE{displaystyle mu _{E}} beigelegt werden, dann sind die Voraussetzungen der IAU-Definition also erfüllt, wenn die in AE gemessene große Halbachse der Erdbahn den Zahlenwert 1,000000036 erhält. Jene Längeneinheit, in der die große Halbachse gemessen werden muss, um diesen Zahlenwert anzunehmen, ist die mit den aktuellen Werten von UE{displaystyle U_{E}} und μE{displaystyle mu _{E}} kompatible aktuelle AE. Gelingt es, die Länge der großen Halbachse in Metern zu ermitteln, so ist über diesen Zusammenhang die Länge der AE in Metern bekannt.

Heliozentrische Gravitationskonstante |

Rechnet man Umlaufzeit Uf{displaystyle U_{f}} und große Halbachse af=1AE{displaystyle a_{f}=1,mathrm {AE} } des fiktiven masselosen Körpers von astronomischen Maßeinheiten wieder nach SI-Einheiten um

1d=86400 s{displaystyle 1,mathrm {d} =86400 mathrm {s} },

(31)

1AE=L m{displaystyle 1,mathrm {AE} =L mathrm {m} }

(32)

und setzt das Ergebnis in Gleichung  (1) ein, so ergibt sich:

(Uf⋅86400sd)2(1AE⋅LmAE)3=4π2G⋅M⊙{displaystyle {frac {(U_{mathrm {f} }cdot 86400,mathrm {frac {s}{d}} )^{2}}{(1,mathrm {AE} cdot L,mathrm {frac {m}{AE}} )^{3}}}={frac {4,pi ^{2}}{Gcdot M_{odot }}}}

(33)

wobei L{displaystyle L} der noch zu bestimmende Umrechnungsfaktor von Astronomischen Einheiten in Meter ist. Einsetzen von

Uf=2πk{displaystyle U_{mathrm {f} }={frac {2pi }{k}}}

(34)

und Auflösen nach GM⊙{displaystyle GM_{odot }} liefert:

GM⊙=k2⋅(LmAE)3(86400sd)2{displaystyle GM_{odot }=k^{2}cdot {frac {(L,mathrm {frac {m}{AE}} )^{3}}{(86400,mathrm {frac {s}{d}} )^{2}}}}

(35)

(Die heliozentrische Gravitationskonstante GM⊙{displaystyle GM_{odot }} ist das Produkt aus der newtonschen Gravitationskonstanten G{displaystyle G} und der Sonnenmasse M⊙{displaystyle M_{odot }}. Sie lässt sich aus der Vermessung der Planetenbahnen ableiten und ist mit wesentlich höherer Genauigkeit bekannt als ihre beiden Einzelfaktoren.)

Die eben genannte Formel stellt nichts anderes dar als die Umrechnung von k² (in astronomischen Maßeinheiten) nach G{displaystyle G} bzw. GM⊙{displaystyle GM_{odot }} (in SI-Einheiten). In astronomischen Maßeinheiten hat k{displaystyle k} stets denselben von der Definition der AE festgelegten Zahlenwert. In SI-Einheiten hängt der Zahlenwert von GM⊙{displaystyle GM_{odot }} ab von dem jeweils aktuellen durch Beobachtung bestimmten Zahlenwert für die Länge L{displaystyle L} der Astronomischen Einheit.

Nicht vorgesehen ist in der 1976er Definition eine eventuelle physikalisch reale Veränderlichkeit von GM⊙{displaystyle GM_{odot }}, etwa durch eine kosmologische Veränderlichkeit von G{displaystyle G} oder den Masseverlust der Sonne. Sollte es infolge gesteigerter Messgenauigkeit notwendig werden, ein zeitlich veränderliches GM⊙{displaystyle GM_{odot }} zu beschreiben, so könnte dies (da k{displaystyle k} ja laut Definition auf seinem gegebenen Zahlenwert fixiert ist) nur durch die sehr unbefriedigende^[7] Verwendung einer zeitlich veränderlichen AE geschehen.

Die Neudefinition der AE von 2012 entkoppelt GM_☉ und AE und eröffnet so den Weg zur direkten Messung von GM⊙{displaystyle GM_{odot }} (und seiner eventuellen Veränderlichkeit) in SI-Einheiten. Der Umweg über die AE ist nicht mehr nötig. Eine Änderung des Zahlenwertes L{displaystyle L} der AE infolge einer Neubestimmung hat keine Änderung des Zahlenwertes von GM⊙{displaystyle GM_{odot }} mehr zur Folge.

Messung |

Um die Länge der AE in Metern zu ermitteln, war es notwendig, die in AE bekannten Entfernungen zu den Planeten oder zur Sonne in Metern zu messen. Dies konnte bis etwa zur Mitte des 20. Jahrhunderts nur durch Triangulationen mit optischen Mitteln geschehen. Die AE wurde hauptsächlich aus hochgenauen Winkelmessungen (Parallaxen) abgeleitet, die von möglichst weit voneinander entfernten Sternwarten aus zu den Planeten Venus und Mars sowie zu erdnahen Asteroiden durchgeführt wurden. Ein kurzer Überblick über diese Bestimmungen der AE bis ins frühe 20. Jahrhundert findet sich im →Artikel Venustransit.

Seit einigen Jahrzehnten können Entfernungen im Sonnensystem direkt gemessen werden. Der moderne Wert der AE wurde mittels Radar- und anderen Distanzmessungen von der Erde zu den Nachbarplaneten und zu Raumsonden bestimmt. Aus der Vermessung der „mittleren Bewegungen“ (d. h. der mittleren Geschwindigkeiten) oder der Umlaufperioden der Planeten, welche sich sehr genau bestimmen lassen, folgen über das Dritte Keplergesetz (in der newtonschen Fassung inklusive relativistischer Korrekturen^[19]) mit derselben Genauigkeit die großen Halbachsen der Planeten in AE. Die Abstandsmessungen zu den Planeten mittels Radar bestimmen deren Bahngeometrie und damit die großen Halbachsen ihrer Bahnen in Metern; das Verhältnis zur Länge der großen Halbachsen in AE liefert die Länge der AE in Metern sowie den Zahlenwert von GM⊙{displaystyle GM_{odot }} in m3/s2{displaystyle mathrm {m^{3}!/s^{2}} }.^[20]

Die folgende Tabelle listet unter anderem einige moderne Ephemeriden auf, die durch Anpassung der physikalischen Bewegungsgleichungen an umfangreiches Beobachtungsmaterial gewonnen wurden. Jede solche Anpassung liefert unter anderem wie eben beschrieben einen Zahlenwert für den Skalenfaktor des Sonnensystems, welcher die Länge der AE in Metern angibt (die jeweils genannten Unsicherheiten sind in der Regel formale Unsicherheiten, die im Zuge der Anpassung aus der Konsistenz der Messdaten untereinander abgeschätzt werden und die meist zu optimistisch ausfallen. Ein realistischeres Bild der Unsicherheiten gewinnt man durch Vergleich der Ergebnisse untereinander):

Die Ephemeride DE405 des JPL liegt derzeit zahlreichen Jahrbüchern und sonstigen Ephemeridenwerken zugrunde. Der aus ihr abgeleitete Zahlenwert von 149 597 870 691 m für die AE war daher für mehrere Jahre der gebräuchlichste Standardwert. Er wurde vom IERS empfohlen.^[34]

Streng genommen ist der genannte Zahlenwert nicht der SI-Wert, da den Berechnungen der Planetenbewegungen die auf den Schwerpunkt des Sonnensystems bezogene Zeitskala TDB zugrunde gelegt wird, während die SI-Sekunde sich definitionsgemäß auf die Erdoberfläche (genauer: das Geoid) bezieht und aus relativistischen Gründen etwas schneller läuft. Rechnet man den TDB-Wert auf strikte SI-Einheiten um, so ergibt sich:^[35]

Die 27. Generalversammlung der Internationalen Astronomischen Union beschloss im Jahre 2009, im Rahmen des „IAU 2009 System of Astronomical Constants“^[6][36] den aus damaligen besten Messungen abgeleiteten Mittelwert von 149 597 870 700 m ± 3 m^[33] zur allgemeinen Verwendung zu empfehlen.

Die 28. Generalversammlung der Internationalen Astronomischen Union beschloss im Jahre 2012, von der bisherigen Definition abzugehen (nach welcher die Länge der Astronomischen Einheit in Metern stets das Ergebnis einer Messung gewesen war) und die Astronomische Einheit einfach als eine Strecke der Länge 149 597 870 700 m (exakt) neu zu definieren.

Veränderlichkeit der gaußschen AE |

Die im Jahre 2012 neu definierte AE ist durch einen festen Zahlenwert festgelegt und damit per Definition unveränderlich. Die über die Gaußsche Konstante definierte frühere AE jedoch ist ein durch Messung zu bestimmender Skalenfaktor des Sonnensystems, der möglicherweise Veränderungen des Sonnensystems widerspiegelt. Messungen zur Bestimmung der AE im früheren Sinne können daher durchaus zur Aufdeckung solcher eventueller Veränderungen noch nützlich sein.

Auswertungen von Radarmessungen scheinen anzudeuten, dass der Skalenfaktor des Sonnensystems langsam zunimmt. Es werden Änderungsraten von 15 ± 4 Meter/Jahrhundert^[37], 7 ± 2 Meter/Jahrhundert^[38] und 1,2 ± 1,1 Meter/Jahrhundert^[39] genannt; die Ursache ist bislang unbekannt.

• Die naheliegende Vermutung, der beobachtete Effekt werde durch die Expansion des Universums verursacht, erweist sich als unzutreffend. Theoretische Untersuchungen anhand gängiger kosmologischer Modelle zeigen, dass die kosmische Expansion keine messbaren Auswirkungen auf die Bewegung der Planeten hat.^[37]
  


• Der durch den Sonnenwind und die Energieabstrahlung verursachte Massenverlust der Sonne führt zu einer langfristigen Vergrößerung der Planetenbahnradien um etwa 0,3 Meter/Jahrhundert.^[37] Dieser Effekt verursacht zwar aufgrund der Abnahme der von der Sonne ausgeübten Gravitationskraft eine Vergrößerung der Abstände der Planeten von der Sonne und untereinander, aufgrund der Abnahme der Sonnenmasse M_☉ jedoch gleichzeitig wegen Gleichung  (34) eine Verringerung^[40] der über die Gaußsche Konstante definierten AE.


• Eine Abnahme der Gravitationskonstanten G{displaystyle G} um etwa 2 · 10⁻¹⁰ Prozent pro Jahr könnte den Effekt erklären, jedoch kann nach neueren Messungen eine eventuelle Veränderlichkeit von G nicht größer als etwa 0,06 · 10⁻¹⁰ Prozent pro Jahr sein.^[31]
  

Bislang lässt sich nicht ausschließen, dass es sich lediglich um systematische Fehler in den Beobachtungen handelt.^[37][38][39] Bei der Berechnung der Planetenbahnen oder der Signalausbreitung unberücksichtigt gebliebene Effekte werden für weniger wahrscheinlich gehalten.^[37] Erklärungsversuche im Rahmen exotischerer Gravitationstheorien wie zum Beispiel der Stringtheorie werden derzeit als „hoch spekulativ“ angesehen.^[41]

Literatur |

• E. M. Standish: The Astronomical Unit now. Proceedings IAU Colloquium No. 196, 2004, S. 163–179 (online, PDF, 1,5 MB).

Einzelnachweise |

1. 
   ↑ Das Internationale Einheitensystem (SI). Deutsche Übersetzung der BIPM-Broschüre „Le Système international d’unités/The International System of Units (8e édition, 2006)“. In: PTB-Mitteilungen. Band 117, Nr. 2, 2007 (Online [PDF; 1,4 MB]). 
   


2. 
   ↑ In der EU-Richtlinie 80/181/EWG wird sie nicht erwähnt, ebenso wenig im Bundesgesetz über das Messwesen der Schweiz.
   


3. 
   ↑ The International System of Units. supplement 2014. In: bipm.org. 2014; S. 13 (PDF; 628 KB).
   


4. 
   ↑ ^abcd IAU: Resolutions B1, B2, B3 and B4. Adopted at the General Assembly 2012 (PDF; 122 KB).
   


5. 
   ↑ ^ab The astronomical unit gets fixed. In: nature.com.
   


6. 
   ↑ ^ab IAU: Numerical Standards for Fundamental Astronomy – IAU 2009 System of Astronomical Constants. Abgerufen am 8. Dezember 2014.
   


7. 
   ↑ ^ab N. Capitaine, B. Guinot, S. A. Klioner: Proposal for the Re-definition of the Astronomical Unit of Length Through a Fixed Relation the the SI Metre. In: N. Capitaine (Hrsg.): Proceedings of the Journées 2010 „Systèmes de Référence Spatio-Temporels“. Observatoire de Paris, 2011, ISBN 978-2-901057-67-3, S. 20–23 (PDF; 233 KB).
   


8. 
   ↑ E. V. Pitjeva, N. P. Pitjev: Estimations of changes of the Sun’s mass and the gravitation constant from the modern observations of planets and spacecraft. In: Solar System Research. 2011 (arxiv:1108.0246): GM⊙˙GM⊙=(−5,0±4,1)⋅10−14 pro Jahr (3σ).{displaystyle textstyle {frac {dot {GM_{odot }}}{GM_{odot }}}=(-5{,}0,pm ,4{,}1)cdot 10^{-14} mathrm {pro Jahr} (3sigma ).}
   


9. 
   ↑ A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0, S. 76.
   


10. 
    ↑ C. F. Gauß: Theoria motus corporum coelestium in sectionibus conicis solem ambientium. Perthes, Hamburg 1809, S. 14 (Digitalisat).
    


11. 
    ↑ A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0, S. 113.
    


12. 
    ↑ IAU: Resolutions of the XVIth General Assembly, Grenoble, France, 1976. (PDF; 1,1 MB): „The astronomical unit of length is that length (A) for which the Gaussian gravitational constant (k) takes the value 0.017 202 098 95 when the units of measurement are the astronomical units of length, mass and time. […]“
    


13. 
    ↑ A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0, S. 111.
    


14. 
    ↑ P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. In: University Science Books. Mill Valley 1992, ISBN 0-935702-68-7, S. 722: „[T]he radius of a circular orbit in which a body of negligible mass, and free of perturbations, would revolve around the Sun in 2π/k days, where k is the Gaussian gravitational constant.“
    


15. 
    ↑ IAU: VIth General Assembly – Stockholm, Sweden – 1938. Adopted at the General Assembly 1938 (PDF; 1.22 MB).
    


16. 
    ↑ The Astronomical Almanac for the Year 2006. United States Government Printing Office, Washington 2004, ISBN 0-11-887333-4; S. K7 (Summe der Massen von Erde und Mond).
    


17. 
    ↑ The Astronomical Almanac for the Year 2006. United States Government Printing Office, Washington 2004, ISBN 0-11-887333-4; S. C1.
    


18. 
    ↑ A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin 2000, ISBN 3-11-015148-0, S. 112.
    


19. 
    ↑ X. X. Newhall, E. M. Standish, J. G. Williams: DE 102: a numerically integrated ephemeris of the Moon and planets spanning forty-four centuries. In: Astronomy and Astrophysics. 125, 150–167 (1983) (bibcode:1983A&A...125..150N).
    


20. 
    ↑ X. X. Newhall, E. M. Standish, J. G. Williams: DE 102: a numerically integrated ephemeris of the Moon and planets spanning forty-four centuries. In: Astronomy and Astrophysics. 125, 150–167 (1983) (bibcode:1983A&A...125..150N), S. 162.
    


21. 
    ↑ G. H. Pettengill, H. W. Briscoe, J. V. Evans, E. Gehrel, G. M. Hyde, L. G. Kraft, R. Price, W. B. Smith: A Radar Investigation of Venus. In: Astronomical Journal. Bd. 67 (1962), S. 181–190 (bibcode:1962AJ.....67..181P).
    


22. 
    ↑ D. O. Muhleman, D. B. Holdridge, N. Block: The Astronomical Unit Determined by Radar Reflections from Venus. In: Astronomical Journal. Bd. 67 (1962), S. 191–203 (bibcode:1962AJ.....67..191M).
    


23. 
    ↑ T. Lederle: The IAU (1976) system of astronomical constants. In: Mitteilungen der Astronomischen Gesellschaft. Nr. 48 (1980), S. 59–65 (bibcode:1980MitAG..48...59L).
    


24. 
    ↑ X. X. Newhall, E. M. Standish, J. G. Williams: DE 102: a numerically integrated ephemeris of the Moon and planets spanning forty-four centuries. In: Astronomy and Astrophysics. 125, 150–167 (1983) (bibcode:1983A&A...125..150N), AE S. 160, Unsicherheit S. 150, S. 162.
    


25. 
    ↑ E. M. Standish: The observational basis for JPL’s DE 200, the planetary ephemerides of the Astronomical Almanac. In: Astronomy and Astrophysics. 233, 252–271 (1990) (bibcode:1990A&A...233..252S).
    


26. 
    ↑ P. K. Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. In: University Science Books. Mill Valley 1992, ISBN 0-935702-68-7, S. 302.
    


27. 
    ↑ G. A. Krasinsky u. a.: The Motion of Major Planets from Observations 1769–1988 and Some Astronomical Constants. In: Celestial Mechanics and Dynamical Astronomy. 55, 1–23 (1993) (bibcode:1993CeMDA..55....1K).
    


28. 
    ↑ JPL Interoffice Memorandum IOM 312.F - 98 - 048; August 26, 1998 (online, PDF; 928 KB); Unsicherheit nach Astronomical Almanac 2006, S. K6.
    


29. 
    ↑ E. V. Pitjeva: Progress in the determination of some astronomical constants from radiometric observations of planets and spacecraft. In: Astronomy and Astrophysics. 371, 760–765 (2001) (online,@1@2Vorlage:Toter Link/145.238.203.4 (Seite nicht mehr abrufbar, Suche in Webarchiven)  Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. PDF; 108 KB).
    


30. 
    ↑ JPL Interoffice Memorandum IOM 312.N - 03 - 009; April 24, 2003 (online, PDF; 6,7 MB).
    


31. 
    ↑ ^ab E. V. Pitjeva: Precise determination of the motion of planets and some astronomical constants from modern observations. In: Proceedings IAU Colloquium. No. 196, 2004, S. 230–241 (online, PDF; 190 KB).
    


32. 
    ↑ JPL Interoffice Memorandum IOM 343R - 06 - 002; April 21, 2006 (online, PDF; 1,0 MB).
    


33. 
    ↑ ^ab E. V. Pitjeva, E. M. Standish: Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit. In: Celestial Mechanics and Dynamical Astronomy. Band 103, Heft 4 (April 2009), S. 365–372, doi:10.1007/s10569-009-9203-8.
    


34. 
    ↑ D. D. McCarthy, G. Petit (Hrsg.): IERS Conventions (2003). Verlag des Bundesamtes für Kartographie und Geodäsie, Frankfurt/M. 2004 (online).
    


35. 
    ↑ The Astronomical Almanac for the Year 2006. United States Government Printing Office, Washington 2004, ISBN 0-11-887333-4; S. K6.
    


36. 
    ↑ B. Luzum u. a.: The IAU 2009 system of astronomical constants: the report of the IAU working group on numerical standards for Fundamental Astronomy. In: Celestial Mechanics and Dynamical Astronomy. Bd. 110, Heft 4 (August 2011), S. 293–304 doi:10.1007/s10569-011-9352-4.
    


37. 
    ↑ ^abcde G. A. Krasinsky, V. A. Brumberg: Secular Increase of Astronomical Unit from Analysis of the Major Planet Motions, and its Interpretation. In: Celestial Mechanics and Dynamical Astronomy. 90: 267–288 (2004) doi:10.1007/s10569-004-0633-z.
    


38. 
    ↑ ^ab E. M. Standish: The Astronomical Unit now. In: D. W. Kurtz (Hrsg.): Transits of Venus: New Views of the Solar System and Galaxy. In: Proceedings IAU Colloquium. No. 196, 2004, 163–179 (online, PDF; 1,5 MB).
    


39. 
    ↑ ^ab E. V. Pitjeva, N. P. Pitjev: Estimations of changes of the Sun’s mass and the gravitation constant from the modern observations of planets and spacecraft. In: Solar System Research. 2011 (arxiv:1108.0246): au˙=(1,2±3,2) m/Jhdt. (3σ).{displaystyle textstyle {dot {au}}=(1{,}2pm 3{,}2) mathrm {m/Jhdt.} (3sigma ).}
    


40. 
    ↑ U. Bastian: Das siderische Jahr und die Astronomische Einheit. In: Sterne und Weltraum. 6/2007, S. 9.
    


41. 
    ↑ O. Preuss, H. Dittus, C. Lämmerzahl: Überraschungen vor der Haustür – Ist die Physik innerhalb des Sonnensystems wirklich verstanden? Sterne und Weltraum 4/2007, 27–34.