Ytukyg

Physikalische Größe
Name	Elektrischer Widerstand
Formelzeichen	R,Z,X{displaystyle R,,Z,,X}
Größen- und Einheitensystem Einheit Dimension SI Ω M·L2·I−2·T−3 Gauß (cgs) s·cm−1 L−1·T esE (cgs) s·cm−1 L−1·T emE (cgs) abΩ L·T−1

Der elektrische Widerstand ist in der Elektrotechnik ein Maß dafür, welche elektrische Spannung erforderlich ist, um eine bestimmte elektrische Stromstärke durch einen elektrischen Leiter (Bauelement, Stromkreis) fließen zu lassen. Dabei sind Gleichgrößen zu verwenden oder Augenblickswerte bei mit der Zeit veränderlichen Größen.^[1]

Wenn die Spannung von einem Anschlusspunkt A zu einem Anschlusspunkt B gezählt wird, wird die Stromstärke in dem Leiter positiv gezählt, wenn er von A nach B fließt; der Widerstand kann nicht negativ sein.^[2]

Als Formelzeichen für den elektrischen Widerstand wird in der Regel R{displaystyle R} – abgeleitet vom Lateinischen resistere für „widerstehen“ – verwendet. Der Widerstand hat die SI-Einheit Ohm, ihr Einheitenzeichen ist das Ω (großes Omega).

Schaltzeichen gemäß EN 60617;
Spannung und Stromstärke haben bei diesen Zählrichtungen dasselbe Vorzeichen

Auf historische Zusammenhänge wird im Artikel „ohmsches Gesetz“ eingegangen.

Ohmscher Widerstand |

Grundlegende Zusammenhänge |

Ein elektrischer Widerstand ist dann ein ohmscher Widerstand, wenn sein Wert unabhängig von der Spannung, der Stärke des Stromes und dessen Frequenz ist. An einem solchen Widerstand gilt das ohmsche Gesetz. Wird in einem Liniendiagramm die Spannung U{displaystyle U} über der Stromstärke I{displaystyle I} aufgetragen, entsteht bei einem ohmschen Widerstand eine Ursprungsgerade; die an einem Bauteil mit ohmschem Widerstand abfallende Spannung ist proportional zur Stromstärke im Widerstand mit dem Proportionalitätsfaktor R{displaystyle R}; dieser ist zugleich der Anstieg der Geraden:

U=RI .{displaystyle U=R;I .}

Näherungsweise und mit Einschränkungen kann ein ohmscher Widerstand durch ein Bauelement, im einfachsten Fall einen Metalldraht, realisiert werden. Dieses wird üblicherweise ebenfalls als Widerstand – siehe Widerstand (Bauelement) – bezeichnet.

Wenn durch den Strom im Widerstand ein Spannungsabfall entsteht, wird elektrische Energie
in thermische Energie umgesetzt.

Der Kehrwert des ohmschen Widerstands, also der Proportionalitätsfaktor zwischen Stromstärke und Spannung, heißt elektrischer Leitwert G{displaystyle G} eines Leiters. Es gilt also:

G=1R .{displaystyle G={frac {1}{R}} .}

Berechnung des Widerstands eines Leiters |

Der ohmsche Widerstand eines Körpers lässt sich aus seinen geometrischen Abmessungen und einer Material-Konstante, dem spezifischen Widerstand ρ{displaystyle rho }, berechnen.

Für einen in Längsrichtung durchflossenen geraden Leiter mit konstanter Querschnittsfläche A{displaystyle A} und der Länge l{displaystyle l} gilt:

R=ρ⋅lA.{displaystyle R=rho cdot {frac {l}{A}}.}

Der spezifische Widerstand selbst ist im Allgemeinen von der Temperatur und eventuell noch weiteren Größen abhängig.

Einflusseffekte |

1. Ein Einfluss der Spannung auf den elektrischen Widerstand ist bei hohen Spannungen und hohen Widerstandswerten zu beachten in der Größenordnung ΔR/RΔU=−10−51V{displaystyle {tfrac {Delta R/R}{Delta U}}=-10^{-5}{tfrac {1}{mathrm {V} }}},^[3] in neuen Entwicklungen von Messwiderständen bis zwei Zehnerpotenzen weniger.^[4] Vielfach ist er bei nichtlinearen Widerständen, z. B. Halbleitern, zu beobachten; siehe unten. Ein Spannungseinfluss auf den Widerstand einer Glühlampe ergibt sich indirekt über den Temperatureinfluss.


2. Ein Einfluss der Frequenz ergibt sich bei vielen Widerständen erst bei höheren Frequenzen durch den Skineffekt, aber selbst bei 50 Hz kommt der Einfluss in dicken Leiterseilen von Hochspannungs-Freileitungen zum Tragen. Bei Wechselstromwiderständen kann ein Frequenz-Einfluss auch bei niedrigen Frequenzen zu beobachten sein; siehe unten. Zur Abgrenzung wird der frequenzunabhängige Anteil am Widerstand auch als Gleichstromwiderstand bezeichnet.


3. Ein Einfluss der Temperatur ist häufig zu beachten, wie nachfolgend beschrieben:

Die oben aufgestellte Gleichung für den Gleichstromwiderstand eines geraden Leiters wird dann beispielsweise ersetzt durch

R20=ρ20⋅lA,{displaystyle R_{20}=rho _{20}cdot {frac {l}{A}};,}

Beispiele für spezifischen Widerstand und Temperaturkoeffizient bei 20 °C
Material	ρ20{displaystyle rho _{20}} in (Ω·mm2)/m	α20{displaystyle alpha _{20}} in 1/°C
Silber	16 · 10−3	3,8 · 10−3
Kupfer [5]	17 · 10−3	4,3 · 10−3
Nickel [6]	70 · 10−3	6,6 · 10−3

wobei der Index die Celsius-Temperatur kennzeichnet, für die die Größen gelten. In Tabellenbüchern ist die übliche Bezugstemperatur 20 °C. Die Werte sind abhängig von Reinheitsgrad sowie thermischer und mechanischer Behandlung; deshalb sind die Tabellenwerte nur als Richtwerte zu verstehen.

Der Einfluss der Temperatur t{displaystyle t} auf den Widerstand R(t){displaystyle R(t)} lässt sich in einfachen Fällen mit dem Linear-Temperaturkoeffizienten α{displaystyle alpha } und dem Temperaturunterschied Δt=t−tb{displaystyle Delta t=t-t_{b}} darstellen. Dann wird der Zusammenhang durch eine lineare Gleichung beschrieben

R(t)=R(tb)(1+αtb⋅(t−tb)){displaystyle R(t)=R(t_{b})(1+alpha _{t_{b}}cdot (t-t_{b}))}

bei tb=20∘C.{displaystyle t_{b}=20,^{circ }mathrm {C} ;.}

Für die meisten Anwendungen mit metallischen Materialien bei nicht zu großen Temperaturbereichen reicht diese lineare Näherung aus; sonst sind Glieder höherer Ordnung in die Gleichung einzubeziehen. (Ein Beispiel mit Summanden bis zur vierten Potenz siehe Platin im Artikel Widerstandsthermometer.)

Je nachdem, ob der Widerstandswert mit steigender Temperatur größer oder kleiner wird, wird unterschieden zwischen

• 
  Heißleitern oder NTC (engl. Negative Temperature Coefficient; Widerstandswert sinkt) und


• 
  Kaltleitern oder PTC (engl. Positive Temperature Coefficient; Widerstandswert steigt). Generell sind alle Metalle Kaltleiter.

In der Mess- und Regelungstechnik wird die Temperaturabhängigkeit des elektrischen Widerstandes als Messeffekt ausgenutzt, zum Beispiel bei Widerstandsthermometern, thermischen Anemometern, Thermostaten oder Einschaltstrombegrenzern.

Es gibt auch verschiedene spezielle Legierungen, die sich durch einen über weite Temperaturbereiche annähernd konstanten spezifischen elektrischen Widerstand auszeichnen, wie das für einen Messwiderstand erforderlich ist.

Wechselstromwiderstand |

Darstellung |

An einem rein ohmschen linearen Widerstand R{displaystyle R}, der von Wechselstrom durchflossen wird, haben Spannung und Stromstärke denselben Phasenwinkel. Wenn sich allerdings frequenzabhängig der Widerstand ändert und die Phasenlage verschiebt, ist zum ohmschen Anteil am Widerstand eine Komponente X{displaystyle X} hinzugekommen, die auf Spannungs- oder Stromänderungen verzögernd reagiert. Bei sinusförmigem Verlauf von Spannung und Stromstärke wird der Quotient aus den Amplituden oder Effektivwerten als Scheinwiderstand Z{displaystyle Z} bezeichnet. In der komplexen Wechselstromrechnung wird der Scheinwiderstand mit dem Phasenverschiebungswinkel φz{displaystyle varphi _{z}} als Impedanz oder komplexer Widerstand Z_{displaystyle {underline {Z}}} zusammengefasst:

Z_=Z⋅ejφz .{displaystyle {underline {Z}}=Zcdot mathrm {e^{jvarphi _{z}}} .}

In einer anderen Darstellung werden die zwei Komponenten in der komplexen Ebene zueinander rechtwinklig zu Z_{displaystyle {underline {Z}}} zusammengefasst:

Z_=R+jX .{displaystyle {underline {Z}}=R+mathrm {j} X .}

Darin werden R{displaystyle R} als Wirkwiderstand und X{displaystyle X} als Blindwiderstand bezeichnet. Der Wirkwiderstand, welcher nicht phasenverschiebend arbeitet, wird auch als ohmscher Anteil der Impedanz bezeichnet.

Werden die Spannung u{displaystyle u} und die Stromstärke i{displaystyle i} als sinusförmige Größen mit der Frequenz f{displaystyle f} oder der Kreisfrequenz ω=2πf{displaystyle omega =2pi f} in der komplexen Ebene durch Zeiger u_{displaystyle {underline {u}}} und i_{displaystyle {underline {i,}}} dargestellt, so entsteht unter Einbeziehung der Eulerschen Formel

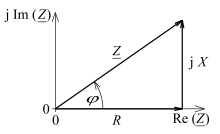
Impedanz als Zeiger in der komplexen Ebene mit ihren Komponenten

Z_=u_i_=u^⋅ej(ωt+φu)ı^⋅ej(ωt+φi)=Z⋅ej(φu−φi)=Z⋅(cos⁡φz+jsin⁡φz){displaystyle {underline {Z}}={frac {underline {u}}{underline {i}}}={frac {{hat {u}}cdot mathrm {e} ^{mathrm {j} (omega t+varphi _{u})}}{{hat {imath }}cdot mathrm {e} ^{mathrm {j} (omega t+varphi _{i})}}}=Zcdot mathrm {e} ^{mathrm {j} (varphi _{u}-varphi _{i})}=Zcdot (cos varphi _{z}+mathrm {j} sin varphi _{z})}

mit

φu−φi=φz .{displaystyle varphi _{u}-varphi _{i}=varphi _{z} .}

Ursachen der komplexen Widerstände |

Bei einer Spule mit der Induktivität L{displaystyle L} gilt

u=L didt .{displaystyle u=L {frac {mathrm {d} i}{mathrm {d} t}} .}

Aufgrund einer Spannung wächst die Stromstärke mit der Zeit an. Bei Wechselstrom folgt dieser verzögert. Mit dem Ansatz in komplexer Schreibweise u_{displaystyle {underline {u}}} und i_{displaystyle {underline {i,}}} wie oben ergibt sich nach der Differenziation

u_=jωL⋅i_{displaystyle {underline {u}}=mathrm {j} omega Lcdot {underline {i}}}

u_i_=jωL=jX .{displaystyle {frac {underline {u}}{underline {i}}}=mathrm {j} omega L=mathrm {j} X .}

Das X{displaystyle X} wird hier als induktiver Blindwiderstand bezeichnet

X=XL=ωL≥0 .{displaystyle X=X_{L}=omega Lgeq 0 .}

Zusammen mit dem Faktor j{displaystyle mathrm {j} } bedeutet das Ergebnis, dass eine Induktivität für sinusförmige Wechselgrößen wie ein phasendrehender Blindwiderstand wirkt.
Mit j=ejπ/2 {displaystyle mathrm {j} =mathrm {e^{jpi /2}} } ergibt sich φz=π/2=+90∘.{displaystyle varphi _{z}=mathrm {pi } /2=+90^{circ }.}

Der Scheinwiderstand einer Induktivität ist ein zur Frequenz proportionaler, aber im Übrigen linearer Widerstand.

Entsprechend gilt bei einem Kondensator mit der Kapazität C{displaystyle C}

u=1C∫idt .{displaystyle u={frac {1}{C}}int imathrm {d} t .}

Aufgrund eines Stromes wächst die Spannung mit der Zeit an. Bei Wechselspannung folgt diese verzögert.
In komplexer Schreibweise und nach der Integration ergibt sich

u_=1jωC⋅i_{displaystyle {underline {u}}={frac {1}{mathrm {j} omega C}}cdot {underline {i}}}

u_i_=1jωC=−j1ωC=jX .{displaystyle {frac {underline {u}}{underline {i}}}={frac {1}{mathrm {j} omega C}}=-mathrm {j} ;{frac {1}{omega C}}=mathrm {j} X .}

Das X{displaystyle X} wird hier als kapazitiver Blindwiderstand bezeichnet

X=XC=−1ωC≤0 .{displaystyle X=X_{C}=-{frac {1}{omega C}}leq 0 .}

Zusammen mit dem Faktor j{displaystyle mathrm {j} } bedeutet das Ergebnis, dass eine Kapazität für sinusförmige Wechselgrößen wie ein phasendrehender Blindwiderstand wirkt. Hier ist φz=−π/2=−90∘.{displaystyle varphi _{z}=-pi /2=-90^{circ }.}

Der Scheinwiderstand einer Kapazität ist ein zur Frequenz umgekehrt proportionaler, aber im Übrigen linearer Widerstand.

Umrechnungen |

Durch Vergleich der Darstellungen

Z_=R+jX=Z⋅(cos⁡φz+jsin⁡φz){displaystyle {underline {Z}}=R+mathrm {j} X=Zcdot (cos varphi _{z}+mathrm {j} sin varphi _{z})}

ergeben sich

Re⁡Z_=Z⋅cos⁡φz=R{displaystyle operatorname {Re} {underline {Z}}=Zcdot cos varphi _{z}=R} (Wirkwiderstand),

Im⁡Z_=Z⋅sin⁡φz=X{displaystyle operatorname {Im} {underline {Z}}=Zcdot sin varphi _{z}=X} (Blindwiderstand)

und für den Scheinwiderstand:

Z=|Z_|=|u_||i_|=u^ı^=ueffieff{displaystyle Z=|{underline {Z}}|={frac {|{underline {u}}|}{|{underline {i}}|}}={frac {hat {u}}{hat {imath }}}={frac {u_{text{eff}}}{i_{text{eff}}}}}

oder

Z=R2+X2{displaystyle Z={sqrt {R^{2}+X^{2}}}}

und für den Phasenverschiebungswinkel zwischen u_{displaystyle {underline {u}}} und i_{displaystyle {underline {i,}}}:

φz=arctan⁡XR .{displaystyle varphi _{z}=arctan {frac {X}{R}} .}

Sonderfälle |

• Für R=0{displaystyle R=0} gilt:

φz=arctan⁡X0{displaystyle varphi _{z}=arctan {frac {X}{0}}} .

• Für X>0{displaystyle X>0} ist φz=+90∘{displaystyle varphi _{z}=+90^{circ }} und Z_=jZ=jX{displaystyle {underline {Z}}=mathrm {j} Z=mathrm {j} X} ;

• für X<0{displaystyle X<0} ist φz=−90∘{displaystyle varphi _{z}=-90^{circ }} und Z_=−jZ=jX{displaystyle {underline {Z}}=-mathrm {j} Z=mathrm {j} X} .

• Für X=0{displaystyle X=0} gilt:

φz=arctan⁡0R=arctan⁡0=0∘{displaystyle varphi _{z}=arctan {frac {0}{R}}=arctan 0=0^{circ }}

Z_=Z=R{displaystyle {underline {Z}}=Z=R} .

Zusammenschaltung, Ersatzwiderstand |

Ersatzschaltbilder für Wechselstromwiderstände
links: Parallelschaltung
rechts: Reihenschaltung

Als Ersatzwiderstand wird der komplexe elektrische Widerstand bezeichnet, der denselben Widerstand besitzt wie eine elektrische Schaltung oder der Teil einer elektrischen Schaltung, den er ersetzt. Ein Ersatzwiderstand kann das Verhalten komplexer elektrischer Anordnungen veranschaulichen und eine Berechnung ermöglichen; siehe auch Ersatzschaltbild.

Tatsächlich auftretende Wechselstromwiderstände lassen sich häufig durch Reihenschaltung oder Parallelschaltung aus einem ohmschen Widerstand mit einer Induktivität oder mit einer Kapazität beschreiben. Welches der Bilder verwendet wird, ist eine Frage der besseren Annäherung an die Wirklichkeit mit möglichst frequenzunabhängigen Größen und der Zweckmäßigkeit für die mathematische Behandlung.

Bei genauer Betrachtung hat aber auch jeder Kondensator einen kleinen induktiven Anteil, so wie eine Spule auch einen kapazitiven Anteil hat. Selbst ein Stück Draht muss exakt mit R{displaystyle R}, C{displaystyle C} und L{displaystyle L} beschrieben werden; siehe auch Leitungsbelag. Dies zeigt sich im Besonderen dann, wenn die Bauelemente mit ihren geometrischen Abmessungen in den Bereich der Wellenlänge der angelegten Wechselspannung kommen; dann besitzen sie eine nicht zu vernachlässigende Induktivität und Kapazität. Sie werden gegebenenfalls zum Schwingkreis, als Beispiel sei hier die Antenne genannt. Deren Enden dürfen als Kondensatorplatten gesehen werden, der Draht dazwischen als Spule.

Werden ein ohmscher Widerstand und ein Blindwiderstand zusammengeschaltet, so können in komplexer Schreibweise die weiter unten folgenden Regeln für Reihen- und Parallelschaltung angewendet werden.

Werden eine kapazitive und eine induktive Impedanz zusammengeschaltet, so entsteht bei genügend kleiner ohmscher Belastung ein Schwingkreis; die Reihen- und Parallelschaltung und die weiteren Konsequenzen werden unter diesem Stichwort behandelt.

Ortskurve |

Ortskurve der Impedanz einer RL-Reihenschaltung

Ortskurve der Impedanz einer RC-Parallelschaltung

Ein anschauliches Hilfsmittel zur Analyse und Beschreibung von Schaltungen mit Wechselstromwiderständen ist die Ortskurve.

Komplexe Größen lassen sich durch Zeiger in der komplexen Ebene darstellen. Wenn die komplexe Größe eine Funktion eines (reellen) Parameters ist und wenn dieser Parameter variiert wird, verschiebt sich die Spitze des Zeigers. Eine Linie durch alle denkbaren Zeigerspitzen wird als Ortskurve bezeichnet.

Die Bilder zeigen Ortskurven der Impedanz als Funktion der Frequenz für die angegebenen Schaltungen. Bei einer RL- oder RC-Reihenschaltung mit einem von der Frequenz unabhängigen ohmschen Widerstand ist auch der Wirkanteil der Impedanz von der Frequenz unabhängig. Bei der entsprechenden Parallelschaltung sind der Wirk- und der Blindanteil der Impedanz ersichtlich beide von der Frequenz abhängig.

Reihen- und Parallelschaltung |

Reihenschaltung |

Werden n{displaystyle n} ohmsche Widerstände hintereinander geschaltet, so addieren sich die Widerstände:

Rrei=∑k=1nRk=R1+R2+⋯+Rn=1G1+1G2+⋯+1Gn{displaystyle R_{text{rei}}=sum _{k=1}^{n}R_{k}=R_{1}+R_{2}+cdots +R_{n}={frac {1}{G_{1}}}+{frac {1}{G_{2}}}+cdots +{frac {1}{G_{n}}}}

Dieses lässt sich an der Reihenschaltung zweier Widerstände veranschaulichen, die sich nur in der Länge l{displaystyle l} unterscheiden.

Die Reihenschaltung ergibt einen Widerstandskörper der Länge l1+l2{displaystyle l_{1}+l_{2}}. Dann gilt:

Rrei=ρ⋅l1+l2A=ρ⋅l1A+ρ⋅l2A=R1+R2{displaystyle R_{text{rei}}=rho cdot {frac {l_{1}+l_{2}}{A}}=rho cdot {frac {l_{1}}{A}}+rho cdot {frac {l_{2}}{A}}=R_{1}+R_{2}}

Bei n{displaystyle n} gleichen Widerständen (Rn=R1=R2=⋯{displaystyle R_{n}=R_{1}=R_{2}=cdots }) ist der Gesamtwiderstand so groß wie der mit der Anzahl der Widerstände multiplizierte Einzelwiderstand:

Rrei=n⋅Rn{displaystyle R_{text{rei}}=ncdot R_{n}}

Der Widerstand einer Reihenschaltung ist stets größer als der größte Einzelwiderstand. Eine Ausnahme gibt es bei Wechselstromwiderständen im Reihenschwingkreis.

Parallelschaltung |

Werden n{displaystyle n} ohmsche Widerstände nebeneinander geschaltet, so addieren sich die Leitwerte beziehungsweise die reziproken Widerstände:

Gpar=G1+G2+⋯+Gn{displaystyle G_{text{par}}=G_{1}+G_{2}+cdots +G_{n}}

1Rpar=∑k=1n1Rk=1R1+1R2+⋯+1Rn{displaystyle {frac {1}{R_{text{par}}}}=sum _{k=1}^{n}{frac {1}{R_{k}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+cdots +{frac {1}{R_{n}}}}

Dieses lässt sich an der Parallelschaltung zweier Widerstände veranschaulichen, die sich nur in ihrer Querschnittsfläche A{displaystyle A} unterscheiden.

Die Parallelschaltung ergibt einen Widerstandskörper der Querschnittsfläche A1+A2{displaystyle A_{1}+A_{2}}. Dann gilt:

Rpar=ρ⋅lA1+A2{displaystyle R_{text{par}}=rho cdot {frac {l}{A_{1}+A_{2}}}}

und umgestellt

1Rpar=A1+A2ρ⋅l=A1ρ⋅l+A2ρ⋅l=1R1+1R2{displaystyle {frac {1}{R_{text{par}}}}={frac {A_{1}+A_{2}}{rho cdot l}}={frac {A_{1}}{rho cdot l}}+{frac {A_{2}}{rho cdot l}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}}

Für die Parallelschaltung gibt es eine alternative Schreibweise mit dem Parallel-Zeichen ‖{displaystyle {|}}:

Rpar=R1‖R2‖⋯‖Rn{displaystyle R_{text{par}}=R_{1}|R_{2}|cdots |R_{n}}

Speziell für zwei parallele Widerstände gilt:

Rpar=R1⋅R2R1+R2{displaystyle R_{text{par}}={frac {R_{1}cdot R_{2}}{R_{1}+R_{2}}}}

Bei n{displaystyle n} gleichen Widerständen ist der Gesamtwiderstand so groß wie der durch die Anzahl der Widerstände dividierte Einzelwiderstand:

Rpar=1nRn{displaystyle R_{text{par}}={frac {1}{n}}R_{n}}

Der Widerstand einer Parallelschaltung ist stets kleiner als der kleinste Einzelwiderstand. Eine Ausnahme gibt es bei Wechselstromwiderständen im Parallelschwingkreis.

Differentieller Widerstand |

Bei nichtlinearen Strom-Spannungs-Kennlinien – wie zum Beispiel von Dioden – ist der Quotient für jedes Strom-Spannungs-Paar unterschiedlich. In diesem Fall gilt das ohmsche Gesetz nicht, und man kann nicht von einem linearen Widerstand R{displaystyle R} sprechen. Kleine Spannungsänderungen sind jedoch näherungsweise proportional zu damit verbundenen kleinen Stromstärkeänderungen. Der Quotient aus kleiner Spannungsänderung und zugehöriger Stromstärkeänderung bei einer bestimmten Spannung wird als differentieller Widerstand r{displaystyle r} bezeichnet. In einem Diagramm, in dem U{displaystyle U} über I{displaystyle I} aufgetragen wird, entspricht er der Steigung der Tangente am betrachteten Punkt der Kennlinie.

r=dUdI{displaystyle r={frac {mathrm {d} U}{mathrm {d} I}}}

Negativer differentieller Widerstand |

Strom- Spannungscharakteristik einer Tunneldiode

Der differentielle Widerstand kann in einem Teil der Kennlinie negativ sein, so dass die Stromstärke bei steigender Spannung sinkt beziehungsweise die Stromstärke bei sinkender Spannung steigt. Im Bild ist das im Bereich U_P < U < U_V der Fall. Ein negativer differentieller Widerstand kann zum Anregen (Entdämpfen) von Schwingkreisen oder zur Erzeugung von Kippschwingungen verwendet werden (Oszillator). Der negative differentielle Widerstand tritt zum Beispiel bei Gasentladungen oder bei Bauteilen wie Avalanche- und Tunneldioden auf, in einfachen elektronischen Schaltungen wie der Lambda-Diode, aber auch bei komplexeren Modulen wie z. B. Schaltnetzteilen auf der Eingangsseite.

Positiver differentieller Widerstand |

Bei positiven differentiellen Widerständen nimmt die Stromstärke mit zunehmender Spannung zu. Alle real existierenden Schaltungselemente besitzen in einem Teil ihrer Kennlinie, jedoch stets für sehr große Werte, einen positiven differentiellen Widerstand. Die meisten Elemente in der Schaltungstechnik besitzen einen ausschließlich positiven differentiellen Widerstand.

Beispiele: realer Widerstand, Diode, Zener-Diode, alle halbleitenden Keramiken.

Der elektrische Widerstand im Teilchenmodell |

Die physikalische Beschreibung benutzt die Vorstellung, dass sich die Valenzelektronen im Metall wie ein Gas (Elektronengas) verhalten. Im einfachsten Modell bildet das Metall ein positiv homogen geladenes Volumen, in denen sich die Elektronen frei bewegen können. In dieses Volumen sind die Atomrümpfe eingebettet, die aus dem Atomkern und den stärker gebundenen Elektronen auf den tieferen, vollbesetzten Schalen bestehen.

Ohne äußere elektrische Spannung bewegen sich die Elektronen ungeordnet im Metall (siehe brownsche Bewegung). Legt man nun eine Spannung an, so werden die freien Elektronen durch das elektrische Feld in Richtung der Feldlinien beschleunigt. Es fließt ein elektrischer Strom.

Auf ihrem Weg durch das Metall kommt es zu elastischen Stößen der Elektronen mit anderen Elektronen, den Atomrümpfen und Phononen. Dabei geben die Elektronen Energie an ihre Stoßpartner ab, werden gestreut und wieder durch das elektrische Feld beschleunigt. Die Elektronen werden durch diese Wechselwirkung dauernd abgebremst und es stellt sich eine mittlere Strömungsgeschwindigkeit ein.

Die bei diesen Stößen an die Atomrümpfe beziehungsweise Phononen übertragene Energie führt zu einer größeren Eigenschwingung um ihre Gleichgewichtslage, ihre Temperatur erhöht sich. Durch die stärkeren Schwingungen erhöht sich die Querschnittsfläche für mögliche Stöße, deren Anzahl mit steigender Temperatur zunimmt und den Widerstand steigen lässt (Kaltleiter). Der Leitungsvorgang in Heißleitern kann mit diesem Modell nicht vollständig erklärt werden, da es hier mit steigender Temperatur zu einer deutlichen Ladungsträgergeneration kommt, die den eben beschriebenen Vorgang überlagern.

Bei sehr hohen Temperaturen, bei denen die Atome des Materials ionisiert werden (Plasma), ist jeder Stoff elektrisch leitend, da die vorher gebundenen Elektronen nun für den Ladungstransport zur Verfügung stehen. Umgekehrt sind Metalle und Oxide bekannt, für die der elektrische Widerstand bei sehr niedrigen Temperaturen unterhalb einer spezifischen Sprungtemperatur verschwindet: Supraleiter besitzen bei Gleichstrom keinen ohmschen Widerstand, Strom fließt bei dieser tiefen Temperatur ohne Verluste.

Durch die thermische Bewegung der Elektronen entsteht ein temperaturabhängiger Rauschstrom, der als Widerstandsrauschen bezeichnet wird.

Hall-Effekt |

Der Hall-Widerstand gibt das Verhältnis Spannung zu Stromstärke eines Hallelementes bei einer bestimmten magnetischen Flussdichte an, wobei diese Spannung quer zur Stromdichte auftritt. Er charakterisiert das Hall-Element bzw. die magnetische Flussdichte, hat jedoch mit dem elektrischen Widerstand dieses Hall-Elementes nichts zu tun.

Der Quanten-Hall-Effekt äußert sich dadurch, dass bei tiefen Temperaturen und starken Magnetfeldern die senkrecht zur Stromdichte auftretende Spannung nicht wie beim klassischen Hall-Effekt linear mit der Flussdichte anwächst, sondern in Stufen. Dieses Phänomen führt auf eine universelle Naturkonstante, die „Von-Klitzing-Konstante“ von der Dimension Widerstand. Da die Von-Klitzing-Konstante relativ einfach gemessen werden kann, wurde vorgeschlagen, sie als Normal für Messungen des elektrischen Widerstands zu verwenden.

Weblinks |

• 
  Versuche und Aufgaben zum elektrischen Widerstand (Wayback Machine Archive) (LEIFI)


• 
  Bewahrung und Darstellung der Einheit des elektrischen Widerstandes Ohm. Exponat-Informationsblatt der Physikalisch-Technischen Bundesanstalt, Hannover Messe '82, 21. April 1982

Einzelnachweise |

1. 
   ↑ EN 80000-6, Größen und Einheiten − Teil 6: Elektromagnetismus, 2008; Eintrag 6-46.
   


2. 
   ↑ IEC 60050, siehe DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch, Eintrag 131-12-04.
   


3. 
   ↑ Wolfgang Gruhle: Elektronisches Messen: Analoge und digitale Signalbehandlung. Springer, 1987, S. 95
   


4. 
   ↑ Datenblatt für Hochspannungswiderstände
   


5. 
   ↑ Datenblatt für Cu 99,9 %
   


6. 
   ↑ Datenblatt für Ni 99,98 %