Ytukyg

Physikalische Größe
Name	Kraft
Formelzeichen	F{displaystyle F}, K{displaystyle K}
Größen- und Einheitensystem Einheit Dimension SI N = kg·m·s−2 M·L·T−2 cgs dyn = g·cm·s−2 M·L·T−2

Kraft ist ein grundlegender Begriff in der Physik. In der klassischen Physik versteht man darunter eine Einwirkung, die einen Körper verformen und/oder beschleunigen kann. Kräfte sind zum Beispiel erforderlich, um Arbeit zu verrichten, wobei sich die Energie eines Körpers oder eines physikalischen Systems ändert. Die Kraft ist eine gerichtete physikalische Größe, die durch einen Vektor dargestellt werden kann. Für zwei Kräfte, die am gleichen Punkt angreifen, gilt: sie sind im Gleichgewicht und heben sich auf, wenn sie entgegengesetzt und gleich groß sind. Allgemein gilt, dass sie zu einer resultierenden Kraft zusammengefasst werden können, die nach dem Kräfteparallelogramm gebildet wird. Kräfte haben verschiedene Ursachen oder Wirkungen und werden teilweise nach ihnen benannt, etwa die Reibungskraft, die Fliehkraft und die Gewichtskraft. Manche Arten von Kräften wurden auch nach Personen benannt, die wesentlich an ihrer Erforschung mitgewirkt haben, wie die Coulombkraft oder die Lorentzkraft.

Die SI-Einheit für Kraft ist das Newton. Das Formelzeichen der Kraft ist meist F{displaystyle F} (von lat. fortitudo oder engl. force)^[1] oder seltener K{displaystyle K} nach dem deutschen Wortanfang.

Der physikalische Kraftbegriff geht wesentlich auf Isaac Newton zurück, der im 17. Jahrhundert in den drei newtonschen Gesetzen die Grundlagen der klassischen Mechanik schuf. Dabei definierte er die Kraft als zeitliche Änderung des Impulses^[2] und identifizierte sie als Ursache für jede Veränderung des Bewegungszustandes eines Körpers. Außerdem erkannte er, dass jeder Körper, der auf einen anderen eine Kraft ausübt, von diesem eine entgegen gerichtete, gleich große Reaktionskraft erfährt.

In der Quantenphysik wird der Begriff Kraft auch in einem übertragenen Sinn verwendet, gleichbedeutend mit dem Begriff Wechselwirkung und losgelöst von der Darstellung durch einen mechanischen Kraftvektor. Es gibt vier „fundamentale Wechselwirkungen“, die auch als Grundkräfte der Physik bezeichnet werden. Sie bilden die Ursache nicht nur aller bekannten Erscheinungsformen der Kräfte, sondern auch aller in der Physik bekannten Prozesse. Eine der vier Grundkräfte, die Gravitation, wird in der allgemeinen Relativitätstheorie durch die Krümmung der Raumzeit beschrieben. Die drei anderen Grundkräfte werden im Standardmodell der Teilchenphysik durch den Austausch von Eichbosonen erklärt, die häufig auch als „Kraftteilchen“ bezeichnet werden.

Wort- und Begriffsgeschichte |

Das Wort „Kraft“ |

Das Wort „Kraft“ ist urgermanischen Ursprungs^[3] und verband sich mit einer Muskelanspannung.^[4] Heute bezeichnet „Kraft“ außerhalb der physikalischen Fachsprache oft eine körperliche oder geistige Eigenschaft, die einem bestimmten Träger zukommt. Dadurch, dass er diese »Kraft hat«, ist er zu bestimmten Handlungen befähigt und kann damit bestimmte Wirkungen erzielen. Beispiele sind Muskelkraft, Geisteskraft, politische Kraft, kraftvolle Stimme, kraftvolle Sprache etc. Andere Formulierungen wie »eine Kraft ausüben«, »unter der Kraft zusammenbrechen«, richten sich mehr auf den Ablauf der Handlung und kommen damit dem physikalischen Fachbegriff näher.

Seit etwa dem Ende des 18. Jahrhunderts kann »Kraft« auch die Personen selbst meinen, die die Träger der Kraft sind (»Streitkräfte«, »Arbeitskräfte«, »Lehrkräfte« etc.).

In der Rechtssprache bedeutet Kraft schon im Althochdeutschen^[4] „Gültigkeit“ bzw. „Wirksamkeit“, was sich heute nur noch in bestimmten Formeln ausdrückt: »in/außer Kraft bleiben/treten/setzen« (vgl. rechtskräftig). Durch Verkürzung entstand aus »in/durch Kraft« die Präposition »kraft« (stets mit dem Genitiv), wie etwa »kraft seines Amtes« oder in der Formulierung »… hat das deutsche Volk kraft seiner verfassungsgebenden Gewalt …« aus der Präambel zum Grundgesetz.

Das griechische Wort für Kraft, δύναμις, lebt fort in Dynamik, was heute die Lehre von der Bewegung unter dem Einfluss von Kräften bezeichnet. Es liegt auch der Krafteinheit dyn des CGS-Systems zugrunde. In der physikalischen Fachsprache ist Kraft (beziehungsweise force) spätestens im 17. Jahrhundert mit dem lateinischen vis gleichgesetzt worden.^[5]

Die Wurzeln des allgemeinen und des mechanischen Begriffs der Kraft |

Aristoteles

Der Ursprung des Kraftbegriffs liegt (nach Max Jammer) in der menschlichen Erfahrung, dass eine einmal gefasste Absicht in die Tat umgesetzt werden kann. Damit steht der Kraftbegriff von Anfang an in engster Verbindung zum Kausalprinzip: Das Ausüben der Kraft ist Folge des Entschlusses, die hervorgebrachte Wirkung ist Folge des Einwirkens der Kraft. Ausgehend von den einfachsten Beispielen, wie willentliches Bewegen der Teile des eigenen Körpers oder anderer Gegenstände, werden dann verallgemeinernd alle Vorgänge, die einen unterstellten „natürlichen“ Zustand oder Ablauf der Dinge verändern, auf das Einwirken von Kräften zurückgeführt. Das schließt auch den Fall der Verhinderung eines natürlich ablaufenden Vorgangs ein, etwa wenn das „natürliche“ Herabfallen eines Gegenstands durch Anwendung einer Kraft verhindert werden kann. Für unerklärbare Vorgänge wurden, wahrscheinlich schon seit prähistorischen Zeiten, jeweils bestimmte Kräfte verantwortlich gemacht. Sie wurden herbeigesehnt oder gefürchtet, und teils in Gestalt von Göttern der verschiedensten Rangstufen personifiziert, angerufen und verehrt.

Physikalische Kräfte im engeren mechanischen Sinne wurden seit der Antike im Zusammenhang mit Problemen von Ruhe und Bewegung der Körper diskutiert. Die Statik behandelte die Frage, welche Kräfte anzuwenden sind, um einen Körper in Ruhe (oder im Gleichgewicht) zu halten. Schon in der Antike entdeckte Archimedes hierzu das Archimedische Prinzip als Gesetz des hydrostatischen Auftriebs und das Hebelgesetz. Das Gleichgewicht von drei Kräften wurde erst im 16. Jahrhundert von Simon Stevin durch die Bedingung des geschlossenen Kräftedreiecks angegeben. Dies ist zum heute allgemein bekannten Kräfteparallelogramm äquivalent. Stevin leitete auch als Erster die Gleichgewichtsbedingung auf der schiefen Ebene her.^[6] Damit wurden die „vier einfachen Maschinen“ in den Universitätslehrbüchern der Physik bis ins 19. Jahrhundert hinein ausführlich dargestellt.

Für Bewegungen von Körpern war seit Aristoteles die Ansicht vorherrschend,^[7] dass eine Kraft nur nötig sei, um einen Körper von seiner natürlichen Form der Bewegung abzubringen, sodass er eine erzwungene Bewegung ausführt. Als natürliche Bewegung galt bei Himmelskörpern die Kreisbahn, bei irdischen Körpern der freie Fall. Eine erzwungene Bewegung, wie z. B. der schiefe Wurf oder die Pendelschwingung, endet automatisch, sobald die bewegende Kraft aufhört zu wirken. Die Einwirkung der bewegenden Kraft konnte nicht als Fernwirkung erfolgen, sondern nur auf mechanische Weise, d. h. durch Stoß, Zug oder Reibung bei unmittelbarem Kontakt von zwei Körpern. Beim geworfenen Stein wurde angenommen, dass es die umgebende Luft ist, die ihn weiter vorantreibt. Die Kraft bestimmt auch die Geschwindigkeit des in Bewegung befindlichen Körpers in einer Weise, die später als eine Proportionalität zur bewirkten Geschwindigkeit gedeutet wurde.^[8] Eine gleichmäßig einwirkende Kraft wurde als eine rasche Folge unmerklich kleiner Stöße angesehen.

Im Mittelalter entstanden aus der aristotelischen Lehre unterschiedliche Bewegungslehren, die schließlich in der Impetustheorie aufgingen. Demnach wird dem Körper durch einen Stoß oder Wurf zu Beginn der Bewegung ein Impetus mitgegeben, der ihn vorantreibt. Dieser dem Körper eingeprägte und in ihm befindliche Impetus erschlafft mit der Zeit, was durch den Widerstand des Mediums, zum Beispiel Luft, verstärkt wird. So endet auch in der Impetustheorie jede Bewegung automatisch, wenn der Impetus verbraucht ist und der Körper »keine Kraft mehr hat«. Im Gegensatz zur Sicht von Aristoteles war nun kein fortdauerndes Einwirken des externen Bewegers mehr nötig. Beibehalten wurde aber beispielsweise die Proportionalität von eingeprägtem Impetus und Geschwindigkeit.

Der heutige physikalische Kraftbegriff löste sich davon ab, als in der Renaissance im 16./17. Jahrhundert die Bewegungen von irdischen und himmlischen Körpern durch genauere und messende Beobachtungen erforscht wurden. Dabei stellte sich heraus (u. a. durch Nikolaus Kopernikus, Galileo Galilei, Johannes Kepler), dass diese Bewegungen einfachen Regeln folgen, die von Isaac Newton durch ein gemeinsames Bewegungsgesetz erklärt werden konnten, wenn man einen neuen Kraftbegriff zugrunde legt. Newtons Kraftbegriff, der zur Grundlage der klassischen Mechanik wurde,^[9] geht vollständig von der Bewegung aus. Er bestimmt als Maß der eingeprägten Kraft die Abweichung von der reinen Trägheitsbewegung des Körpers, die ihrerseits als geradlinig gleichförmig vorausgesetzt wurde. Damit verlor auch das Gewicht die Eigenschaft einer dem einzelnen Körper innewohnenden Eigenschaft und wurde zu einer eingeprägten Kraft, deren Stärke über die Fallbeschleunigung bestimmt werden konnte. Allerdings benutzt Newton selbst, wie auch seine Nachfolger, noch bis ins 19. Jahrhundert, das Wort Kraft an manchen Textstellen auch in anderem Sinn, seine „Trägheitskraft“ ähnelt z. B. zuweilen dem Impetus.

Der moderne Begriff der mechanischen Kraft |

Galileo Galilei

Auch Galilei war von der aristotelischen Tradition geprägt worden, kam aber mit seinem Trägheitsgesetz ihrer Überwindung schon sehr nahe.^{[10](S. 209)} Er erkannte, dass Ruhe und gleichförmige horizontale Bewegung physikalisch nicht wesensverschieden sind (siehe Galilei-Invarianz). Christiaan Huygens leitete mit dieser Erkenntnis anschließend die Erhaltung des Impulses und damit die Gesetze des Stoßes ab. Diese Gesetze zeigten, dass sich gleichförmige Bewegung und Ruhe nicht dadurch unterscheiden, dass für die bloße Aufrechterhaltung der Bewegung eine eigene Kraft nötig sei, für die Beibehaltung der Ruhe aber nicht. Vielmehr macht erst die Veränderung des jeweiligen Bewegungszustandes eine äußere Einwirkung erforderlich. Diese Einwirkung präzisierte wenig später Isaac Newton in seinen Bewegungsgesetzen. Zunächst legte er (wie vor ihm Descartes) den unbeeinflussten Bewegungszustand als geradlinig gleichförmig fest, und definierte in seinem neuen Begriff vis impressa (lat. für „eingeprägte Kraft“) die Geschwindigkeit, mit der dieser Bewegungszustand sich ändert, als Maß der Kraft. Dieser Kraftbegriff gilt nach weiterer Präzisierung durch Leonhard Euler und Jean-Baptiste le Rond d’Alembert noch heute, er gehört zu den Grundlagen der klassischen Mechanik. Newton selbst verwendete den Begriff vis impressa allerdings nicht immer nur in diesem Sinne und benutzte das gleiche Wort vis unter anderem auch als vis inertiae für das Bestreben der Körper, ihren Bewegungszustand beizubehalten, also ihre Trägheit.^{[10](S. 262)}

Daneben wurde das Wort Kraft bis weit ins 19. Jahrhundert auch in anderen physikalischen Bedeutungen benutzt, die ebenfalls nicht durch die newtonsche Definition gedeckt waren, z. B. in der Bedeutung der heutigen Begriffe von Impuls und Energie. Bis sich der moderne Energiebegriff herausgebildet und durchgesetzt hatte, wurde beispielsweise die kinetische Energie mit dem von Gottfried Wilhelm Leibniz geprägten Ausdruck der »lebendigen Kraft« (vis viva) bezeichnet, der noch im 19. Jahrhundert von Hermann von Helmholtz und Anfang des 20. Jahrhunderts in der technischen Mechanik verwendet wurde. Das setzt sich bis heute fort in Worten wie »Kraftwerk« und »Kraftfahrzeug« für Maschinen, die Energie bereitstellen.^[4]

„Kraft“ in der Naturlehre und Naturphilosophie |

Kraft war neben dem in der newtonschen Mechanik präzisierten Begriff auch einer der allgemeinsten Grundbegriffe der Naturlehre. Die Naturlehre bildete bis in die erste Hälfte des 19. Jahrhunderts das Sammelbecken der beschreibenden Naturwissenschaften und damit auch die empirische Grundlage der Naturphilosophie. Darin galten die Kräfte, die ein Ding besitzt, als die Ursache jeder Veränderung oder Wirkung, die es hervorbringen kann. Die Kräfte eines Dings wurden als Inbegriff seiner Natur gesehen, wobei Natur nach der ursprünglichen Bedeutung des Wortes alles bezeichnete, was nicht künstlich, also durch menschliche Kunst, hervorgebracht sei.^[11] So musste in der Naturlehre auch für die reine Ortsveränderung eines Körpers eine Ursache in Gestalt einer ständig einwirkenden Kraft angegeben werden. Im Falle der gleichförmig-geradlinigen Bewegung war das eine dem Körper eigene „Trägheitskraft“, die nicht mit dem heutigen Begriff einer Trägheitskraft verwechselt werden darf. Eine Beschleunigung oder Richtungsänderung war dann nur durch das gleichzeitige Einwirken einer zusätzlichen zweiten Kraft möglich. Dieser letztlich aus der antiken Philosophie hervorgegangene Kraftbegriff passte zwar gut zu dem Alltagsverständnis, war aber mit der newtonschen Mechanik unvereinbar. Dennoch findet er sich in Deutschland selbst in physikalischen Lehrbüchern bis spät ins 19. Jahrhundert, zweihundert Jahre nach Newton und hundert Jahre nachdem die newtonsche Mechanik sich durch ihre unbestreitbaren Erfolge durchgesetzt und damit zur ersten allseits anerkannten exakten Naturwissenschaft entwickelt hatte.^[12]

Kritik des Begriffs der mechanischen Kraft |

Die newtonsche Mechanik und insbesondere ihr Kraftbegriff wurden von Anfang an mit verschiedenen Begründungen kritisiert. Zum einen konnte man damit die Erscheinungen nicht in solcher Weise aus ersten Prinzipien erklären, wie das damals von der Naturphilosophie (und der Philosophie im Allgemeinen) erwartet wurde. Kraft erschien in der newtonschen Mechanik als ein nützlicher, aber lediglich mathematischer Hilfsbegriff zur Analyse und Beschreibung von Bewegungen, der aber die wahren Ursachen eher im Verborgenen lasse. Newton selber hatte dieser Kritik mit dem Satz „Ich mache hierzu keine Hypothesen“ (Hypotheses non fingo, in seinem Hauptwerk Philosophiae Naturalis Principia Mathematica) vorbeugen wollen. Daneben wurden – teils zu Recht – Unklarheiten im Verhältnis zwischen der beschleunigenden Kraft (vis impressa) und der Trägheitskraft (vis inertiae) kritisiert. In der romantischen Naturphilosophie des deutschen Idealismus (Friedrich Schelling, Georg Friedrich Hegel) mündete diese Kritik Anfang des 19. Jahrhunderts in eine anhaltende, grundsätzliche Ablehnung der modernen Naturwissenschaft in der durch Newton begründeten Art.^[13][14]

Ein zweites Gegenargument bestand darin, dass man mit Newtons Kraftbegriff die Gravitation als eine Fernwirkung aufzufassen hätte, die den absolut leeren Raum durchdringen könnte. Newton selbst verwahrte sich heftig gegen diese Schlussfolgerung, denn sie stand im Gegensatz zur traditionellen Auffassung (z. B. bei Descartes), dass kein Körper dort etwas bewirken könne, wo er sich nicht befinde. Selbst noch bei Leonhard Euler^[15] galt die Möglichkeit einer solchen Fernwirkung als eine absurde Annahme.

Weiter wurde im späten 19. Jahrhundert eingewendet (Ernst Mach, Gustav Kirchhoff, Heinrich Hertz), dass der Ursprung des newtonschen Kraftbegriffs im Umfeld des Begriffspaars Ursache-Wirkung liege, das vollständig von der menschlichen Auffassung des Geschehens geprägt sei. Deshalb dürfe der Begriff der Kraft in der Mechanik nicht zu den Grundbegriffen zählen, sondern solle nach Möglichkeit sogar ganz eliminiert werden. Dass dies tatsächlich möglich ist, hatte die Entwicklung der klassischen Mechanik durch (u. a.) Lagrange und Hamilton gezeigt, wonach die Kenntnis der Formeln für die kinetische und potentielle Energie eines mechanischen Systems ausreicht, dessen Bewegungsgleichungen vollständig zu ermitteln. Diesem Weg ist die moderne Quantenmechanik und Quantenfeldtheorie gefolgt. Hier sind Kraft – wenn dieser Begriff im newtonschen Sinn überhaupt noch auftaucht – und selbst die potentielle Energie keine Grundbegriffe, sondern werden unter gewissen, für die klassische Physik charakteristischen Bedingungen als effektive Größen abgeleitet. In der Technischen Mechanik hingegen blieb die zentrale Rolle der Kraft unangefochten.

Grundkräfte der Physik |

Grundlegend für die Herleitung der Kraft als effektive Größe ist in der heutigen Quantenfeldtheorie die Erzeugung und Vernichtung eines Elementarteilchens durch ein anderes aufgrund einer der Fundamentalen Wechselwirkungen. Zu den Bedingungen die dabei eingehalten werden müssen, gehört in jedem Fall die Erhaltung von Gesamtimpuls und Gesamtenergie. Insgesamt kommt das dem früheren Bild, mechanische Kraft sei eine Folge kleiner Stöße, wieder recht nahe. Im erweiterten Sinn des Worts „Kraft“ werden diese fundamentalen Wechselwirkungen, zusammen mit der Gravitation, auch als „Grundkräfte der Natur“ bezeichnet, alle zwischen Körpern bekannten physikalischen Vorgänge können auf sie zurückgeführt werden.

Messung von Kräften |

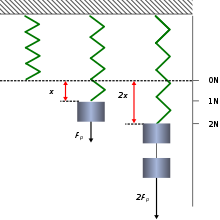
Kraftmessung mit dem hookeschen Gesetz, hier in der Form Fp=D⋅x{displaystyle F_{mathrm {p} }=Dcdot x}

Eine Kraft kann über eine Weg-Zeit-Messung bestimmt werden, wenn sie eine Beschleunigung verursacht. Nach dem zweiten newtonschen Gesetz gilt für Körper mit gleichbleibender Masse m{displaystyle m} und konstanter Beschleunigung a{displaystyle a} der Zusammenhang F→=m⋅a→{displaystyle {vec {F}}=mcdot {vec {a}}}. Dieser Zusammenhang kann auch aus der abgeleiteten Einheit Newton (N=kg⋅ms2{displaystyle mathrm {N=kgcdot {tfrac {m}{s^{2}}}} }) abgelesen werden. In der Praxis wird oft aus einem bekannten (vorteilhafterweise linearen) Zusammenhang zwischen der wirkenden Kraft und einer leicht zu messenden Größe auf die Kraft geschlossen. Beispiele hierfür sind die Verformung eines elastischen Materials oder die Änderung des elektrischen Widerstands eines Dehnungsmessstreifens.

Eine Kraft kann auf verschiedene Art durch die von ihr verursachte Verformung bestimmt werden. Im Schulunterricht und in einigen einfachen Anwendungen werden Kräfte mit sogenannten Federkraftmessern über die Längenänderung von Schraubenfedern gemessen. Dabei wird das hookesche Gesetz genutzt, dem zufolge die Ausdehnung geeigneter Federn zur ausgeübten Kraft proportional ist: Es gilt F=D⋅Δl,{displaystyle F=Dcdot Delta l,} wobei Δl{displaystyle Delta l} die Längenänderung der Feder und D{displaystyle D} die Federkonstante bezeichnet.^[16]

Nutzbar ist auch das Hebelgesetz. Damit kann eine unbekannte Kraft durch den Vergleich mit einer bekannten Kraft, zum Beispiel der Gewichtskraft eines Massestücks bestimmt werden. Im einfachsten Fall wird eine Waage benutzt, deren Anzeige mit Hilfe der bekannten Schwerebeschleunigung g{displaystyle g} in die wirkende Kraft umgerechnet werden kann.

Mit dem Rasterkraftmikroskop sind Kräfte auf eine kleine Blattfeder bis etwa 1 pN nachweisbar. Dies lässt sich für die Untersuchung von Oberflächen nutzen.^[17] Kräfte bis in den Bereich von etwa 5⋅10−24N{displaystyle 5cdot 10^{-24},mathrm {N} } sind mit Hilfe einzelner ultrakalter Magnesium-Ionen in Paulfallen über die Synchronisation mit einem externen Radiosignal gemessen worden.^[18]

Kraft als vektorielle Größe |

Darstellung von Kräften |

Kräfte an einem Kragträger

Für die Beschreibung einer Kraft ist nicht nur ihr Betrag (also ihre „Stärke“), sondern auch die Angabe der Richtung notwendig, in der die Kraft wirkt. Solche Größen, festgelegt durch die Angabe von Zahlenwert, Einheit und Richtung, nennt man vektorielle Größen; sie werden gekennzeichnet durch über dem Symbol angebrachte Pfeile. In einem dreidimensionalen kartesischen Koordinatensystem hat ein Kraftvektor drei Komponenten:

F→=(FxFyFz){displaystyle {vec {F}}={begin{pmatrix}F_{x}\F_{y}\F_{z}end{pmatrix}}}

• Um beispielsweise die Gewichtskraft F→G{displaystyle {vec {F}}_{mathrm {G} }} zu beschreiben, mit der ein Körper der Masse m{displaystyle m} von der Erde angezogen wird, kann ein Koordinatensystem mit vertikaler z{displaystyle z}-Achse gewählt werden:

F→G=( 0  0 −mg){displaystyle {vec {F}}_{mathrm {G} }={begin{pmatrix} 0 \ 0 \-mgend{pmatrix}}}

Der Körper wird (mit der Erdbeschleunigung g{displaystyle g}) nach unten beschleunigt, deshalb ist die z-Komponente negativ.

Neben Betrag und Richtung des Kraftvektors bestimmt auch sein Angriffspunkt die Kraftwirkung. Bei starren Körpern dürfen Kräfte entlang ihrer Wirklinie verschoben werden, ohne dass sich ihre Wirkung verändert. Seilkräfte wirken beispielsweise immer in Richtung des Seils (und zwar in Zugrichtung) und haben dieselbe Wirkung unabhängig davon, wie lang das Seil ist. Bei Oberflächen- und Volumenkräften ist die Wirklinie und damit der Angriffspunkt oftmals nicht offensichtlich. Beispielsweise greifen bei einem schwebenden Ballon vereinfacht gesagt die Gewichtskraft im Schwerpunkt an, die Auftriebskraft jedoch im sogenannten Formschwerpunkt, weswegen hier die Wirklinien der beiden Kräfte im Allgemeinen nicht zusammenfallen. Es wirkt so lange ein aufrichtendes Moment auf den Ballon, bis sich sein Schwerpunkt senkrecht unter seinem Formschwerpunkt befindet. Auch dann haben beide Kräfte noch verschiedene Angriffspunkte, liegen jedoch auf einer Wirklinie, sodass sie sich gegenseitig kompensieren können. Darauf beruht die stabile Fluglage von Ballons.

Die Verformung eines Körpers kommt genau genommen nicht durch eine einzelne Kraft zustande, sondern dadurch, dass an verschiedenen Angriffspunkten unterschiedliche Kräfte wirken. Die dadurch entstehenden mechanischen Spannungen können beschrieben werden, indem Kraft als ein vektorielles Feld aufgefasst wird: In jedem Angriffspunkt, bezeichnet durch den Ortsvektor r→{displaystyle {vec {r}}}, kann prinzipiell eine andere Kraft F→(r→){displaystyle {vec {F}}({vec {r}})} wirken. Je nachdem, wie diese Kräfte gerichtet sind, wird der Körper gedehnt, komprimiert oder verzerrt.

Superpositionsprinzip |

Zerlegung der Gewichtskraft G→{displaystyle {vec {G}}} in die Komponenten F1→{displaystyle {vec {F_{1}}}} (Hangabtriebskraft) und F2→{displaystyle {vec {F_{2}}}} (Gegenkraft zur Normalkraft N→{displaystyle {vec {N}}})

Das Superpositionsprinzip der Mechanik, das in Newtons Werk auch als „lex Quarta“ bezeichnet wird, besagt: Wirken auf einen Punkt (oder einen starren Körper) mehrere Kräfte F1→,F2→,…,Fn→{displaystyle {vec {F_{1}}},{vec {F_{2}}},dotsc ,{vec {F_{n}}}}, so addieren sich diese vektoriell zu einer resultierenden Kraft Fres→=F1→+F2→+⋯+Fn→.{displaystyle {vec {F_{mathrm {res} }}}={vec {F_{1}}}+{vec {F_{2}}}+dotsb +{vec {F_{n}}}.} Das heißt, Fres→{displaystyle {vec {F_{mathrm {res} }}}} bewirkt dasselbe wie sämtliche Kräfte F1→,F2→,…,Fn→{displaystyle {vec {F_{1}}},{vec {F_{2}}},dotsc ,{vec {F_{n}}}} gemeinsam.

• Wenn zwei am selben Angriffspunkt angreifende Kräfte F1→{displaystyle {vec {F_{1}}}} und F2→{displaystyle {vec {F_{2}}}} gleich groß, aber entgegengesetzt gerichtet sind, so ist die resultierende Kraft gleich Null. Man spricht dann auch von einem Kräftegleichgewicht.


• Zusammensetzung von Kräften (die im selben Punkt angreifen):
  Wirken zwei Kräfte mit den Beträgen F1{displaystyle F_{1}} und F2{displaystyle F_{2}} in die gleiche Richtung, so addieren sich die Beträge zum Betrag F{displaystyle F} der Gesamtkraft, F=F1+F2{displaystyle F=F_{1}+F_{2}}.
  Wirken zwei Kräfte mit den Beträgen F1{displaystyle F_{1}} und F2{displaystyle F_{2}} in entgegengesetzter Richtung, so resultiert der Betrag F{displaystyle F} der Gesamtkraft dadurch, dass sich der größere Kraftbetrag um den kleineren verringert. Die Richtung der Gesamtkraft stimmt mit der Richtung derjenigen Einzelkraft überein, die den größeren Betrag hat, F=|F1−F2|{displaystyle F=|F_{1}-F_{2}|}.
  Wirken zwei Kräfte in unterschiedlicher Richtung, so ergeben sich Richtung und Betrag der Resultierenden zeichnerisch durch ein Kräfteparallelogramm. Die Kräfte F1→{displaystyle {vec {F_{1}}}} und F2→{displaystyle {vec {F_{2}}}} werden zu einem Parallelogramm ergänzt, die Parallelogramm–Diagonale entspricht der resultierenden Kraft. Die resultierende Kraft mehrerer Kräfte unterschiedlicher Richtung kann zeichnerisch mit einem Kräftepolygon oder rechnerisch als Summe von Vektoren bestimmt werden.


• Zerlegung von Kräften:
  Während sich bei einer horizontalen Ebene die Gewichtskraft G→{displaystyle {vec {G}}} und die Normalkraft N→{displaystyle {vec {N}}} kompensieren, kann das im Fall der schiefen Ebene nicht geschehen. Die Normalkraft wirkt senkrecht zur Ebene nach oben und ist damit der Gewichtskraft nicht genau entgegengerichtet. Um angeben zu können, welcher Teil der Gewichtskraft nicht von der Normalkraft kompensiert wird und somit als Hangabtriebskraft den Körper die schiefe Ebene hinab beschleunigt, kann die Gewichtskraft in zwei Kräfte zerlegt werden. Die eine zeigt zweckmäßigerweise in die Gegenrichtung der Normalkraft (und wird von dieser kompensiert, F2→=−N→{displaystyle {vec {F_{2}}}=-{vec {N}}}), die zweite in Richtung der Ebene – diese stellt die Hangabtriebskraft F1→{displaystyle {vec {F_{1}}}} dar. Über F1→=ma→{displaystyle {vec {F_{1}}}=m,{vec {a}}} kann die Beschleunigung a→{displaystyle {vec {a}}} des Körpers berechnet werden.
  Eine solche Zerlegung ist immer dann korrekt, wenn die Vektorsumme der Teilkräfte die ursprüngliche Kraft ergibt, hier muss also F1→+F2→=G→{displaystyle {vec {F_{1}}}+{vec {F_{2}}}={vec {G}}} gelten.

Krafteinheiten |

Abhängig vom verwendeten Einheitensystem wird jeweils eine andere Maßeinheit für die Kraft verwendet. Statt solcher Einheiten wie Dyn, Kilopond, Pound-force oder Poundal wird im internationalen Einheitensystem (SI) das Newton [.mw-parser-output .IPA a{text-decoration:none}ˈnjuːtn̩] verwendet. Das Newton wurde im Jahre 1946 durch die Generalkonferenz für Maß und Gewicht im heutigen Sinn festgelegt als abgeleitete Einheit der Basiseinheiten Kilogramm (kg), Meter (m) und Sekunde (s):

1N=1kg⋅ms2{displaystyle 1,mathrm {N} =1,{frac {mathrm {kg} cdot mathrm {m} }{mathrm {s} ^{2}}}}

und 1948 von ihr nach Isaac Newton benannt.^[19]

Kraft in der klassischen Mechanik |

Kraft in den Newtonschen Gesetzen |

Sir Isaac Newton

Der newtonsche Kraftbegriff basiert auf folgendem Gedanken: Alle Einwirkungen auf einen Körper, die zu einer Änderung seines Bewegungszustands führen, sind Kräfte. Die Kraft beschreibt die Intensität und Richtung der Wechselwirkung zweier Körper, keine Eigenschaft eines Körpers. Bei einer kräftefreien Bewegung bzw. wenn ein Kräftegleichgewicht vorliegt, ändert sich folglich der Bewegungszustand eines Körpers nicht, er bewegt sich somit geradlinig mit konstanter Geschwindigkeit weiter oder er bleibt in Ruhe. Das ist der Inhalt des Trägheitsprinzips, wie es schon Galilei formulierte.

Das Aktionsprinzip verknüpft die Kraft F→{displaystyle {vec {F}}}, die auf einen freien Körper ausgeübt wird, mit der Änderung seines Impulses p→{displaystyle {vec {p}}}: In jedem infinitesimal kurzen Zeitraum dt{displaystyle mathrm {d} t} ändert sich der Impuls des Körpers um dp→{displaystyle mathrm {d} {vec {p}}} gemäß dp→=F→dt.{displaystyle mathrm {d} {vec {p}}={vec {F}}mathrm {d} t.} Der Impuls eines Körpers ist das Produkt seiner Masse m{displaystyle m} und der Geschwindigkeit v→{displaystyle {vec {v}}}; es gilt p→=mv→.{displaystyle {vec {p}}=m{vec {v}}.} Da die Masse des Körpers in den meisten Fällen praktisch konstant bleibt (Ausnahmen sind beispielsweise Raketen oder Körper bei relativistischen Geschwindigkeiten), schreibt man das zweite newtonsche Axiom meistens in der Form F→=mdv→dt=ma→{displaystyle {vec {F}}=m{tfrac {mathrm {d} {vec {v}}}{mathrm {d} t}}=m{vec {a}}}, wobei a→{displaystyle {vec {a}}} für die Beschleunigung des Körpers steht. Die Kraft auf den betrachteten Körper entspricht also dem Produkt aus seiner Masse und seiner Beschleunigung.

Als Konsequenz der Impulserhaltung folgt zudem das Reaktionsprinzip, wonach stets mit einer Kraft („actio“) vom Körper A auf Körper B, also F→A→B{displaystyle {vec {F}}_{Ato B}}, eine gleich große, aber genau entgegengesetzt gerichtete Kraft („reactio“) von Körper B auf Körper A verbunden ist: F→A→B=−F→B→A.{displaystyle {vec {F}}_{Ato B}=-{vec {F}}_{Bto A}.} Die reactio ist dabei nicht nur eine Art passiver Widerstand, sondern eine Kraft, die aktiv am Wechselwirkungspartner angreift. Sie ist vom Kräftegleichgewicht zu unterscheiden, denn die Angriffspunkte von F→A→B{displaystyle {vec {F}}_{Ato B}} und F→B→A{displaystyle {vec {F}}_{Bto A}} sind verschieden, die beiden Kräfte können einander also nicht kompensieren.

In moderner Schreibweise würde die der newtonschen Intention entsprechende Fassung eher Δp→∼F→⋅Δt{displaystyle Delta {vec {p}}sim {vec {F}}cdot Delta t} lauten. Die Verwendung des Wortes Kraft in Newtons Schriften ist nicht immer eindeutig. Kraft ist meist eher als Kraftstoß F→⋅Δt{displaystyle {vec {F}}cdot Delta t} zu deuten, der einen Zusatzimpuls Δp→{displaystyle Delta {vec {p}}} bewirkt.^[20]

Kräftegleichgewicht als Schlüsselbegriff der Statik |

Wenn an einem Körper mehrere Kräfte F→i{displaystyle {vec {F}}_{i}} angreifen, die sich gegenseitig aufheben, d. h., wenn für die Vektorsumme der Kräfte

∑iF→i=0→{displaystyle sum _{i}{{vec {F}}_{i}}={vec {0}}}

gilt, dann spricht man vom Kräftegleichgewicht. Der betrachtete Körper ändert seinen Bewegungszustand nicht. Früher^[21] wurde diese Tatsache „erster Hauptsatz der Statik starrer Körper“ genannt. Bei den Kräften F→i{displaystyle {vec {F}}_{i}} handelt es sich sowohl um die eingeprägten Kräfte, die durch Wechselwirkung mit anderen Körpern in der Umgebung entstehen, als auch um die inneren Kräfte, die zwischen Teilen des Körpers aufscheinen. Speziell „Zwangskräfte“ treten auf, wenn Teile des Körpers geometrischen Bindungen unterliegen, die beispielsweise durch Stütz- und Haltekräfte eine Beschleunigung des Körpers verhindern. Die Betrachtung des Kräftegleichgewichts ist Inhalt der Statik.

Um hier oder allgemeiner in der Technischen Mechanik Systeme (z. B. Tragwerke) einer Berechnung zugänglich zu machen, werden diese aus ihrer Umgebung frei geschnitten, indem alle ihre Wechselwirkungen mit der Umgebung durch Kräfte und Momente ersetzt werden. Bindungen zwischen den Körpern des Systems und zwischen dem System und seiner Umwelt, die nur geringe Formänderungen zulassen, werden als „starre Bindungen“ idealisiert. Solche starren Bindungen sind in der Regel Gelenke zwischen den Körpern oder Lager. Damit geht der physikalische Charakter dieser Bindungen verloren, und die durch diese Bindungen bedingte mechanische Wechselwirkung der Körper wird durch Zwangskräfte (Lagerreaktionen) repräsentiert. Von ruhenden Starrkörpern ausgeübte Zwangskräfte verrichten am System keine Arbeit, da keine resultierende Bewegung stattfindet. Kräftesysteme können analytisch oder grafisch bearbeitet werden und erfüllen im Gleichgewicht das oben angeführte Kräftegleichgewicht sowie das Momentengleichgewicht, welches früher „zweiter Hauptsatz der Statik starrer Körper“ genannt wurde.^[21]

• Beispiele für eingeprägte Kräfte mit vorgegebenem Verlauf: Gewichtskraft, Druck- und Zugkraft (z. B. Auflast und Windsog), Federkraft, Drehmoment
  


• Beispiele für aus den eingeprägten Kräften resultierende Zwangskräfte: Auflagerkraft, Haftkraft (Reibungskraft)


• Beispiel für innere Kräfte: Gelenkkräfte, wenn der Körper über Gelenke verfügt, Schnittreaktionen
  

Das Prinzip der virtuellen Arbeit besagt, dass in der Statik die Summe der virtuellen (angenommenen) Arbeiten aller Kräfte null ergeben muss, was der „dritte Hauptsatz der Statik starrer Körper“ ist.^[21] Das d’Alembertsche Prinzip erweitert dieses Prinzip auf Systeme der klassischen Dynamik, die Zwangskräften unterworfen sind, und wird zum Aufstellen von Bewegungsgleichungen verwendet.

Festigkeitslehre und Baustatik |

In der Baustatik und Festigkeitslehre werden Einzellasten (Punktlasten) von Streckenlasten (Linienlasten) und Flächenlasten unterschieden. Auch das Eigengewicht als Gewichtslast wird zu Berechnungszwecken häufig zu Einzel-, Linien- oder Flächenlasten vereinfacht.

Volumenkräfte und Oberflächenkräfte |

Freischneiden:
1) Ein Körper wird von der Gravitationskraft Fg{displaystyle F_{mathrm {g} }} nach unten gezogen. Diese Kraft wirkt auf den ganzen Körper und ist eine Volumenkraft. In horizontaler Richtung ist der Körper in Ruhe, die beiden Oberflächenkräfte −Fo{displaystyle -F_{mathrm {o} }} und Fo{displaystyle F_{mathrm {o} }} heben sich gegenseitig auf.
2) Der Körper wurde gedanklich in zwei Untersysteme symmetrisch zerteilt. Auf jedes Untersystem wirkt die halbe Volumenkraft. Da auch beide Untersysteme in horizontaler Richtung in Ruhe sind, müssen an der Schnittfläche zusätzliche Oberflächenkräfte eingezeichnet werden.

Vor allem in der technischen Mechanik unterscheidet man zwischen Volumenkräften und Oberflächenkräften, die auf einen Körper wirken.

Unterschiede beim Freischneiden |

Behandelt man ein komplexes Problem – wie die mechanischen Wechselwirkungen mehrerer Körper untereinander oder zusammengesetzte Körper (z. B. starre oder deformierbare Körper) – so schneidet man das relevante Untersystem gedanklich von seiner Umgebung frei. Nun ordnet man den einzelnen Stücken der Oberfläche des freigeschnittenen Teilsystems die Kräfte zu, mit denen an dieser Stelle das übrige System auf das Teilsystem einwirkt. Mit der entgegengesetzt gleichen Oberflächenkraft wirkt dann auch das freigeschnittene Teilsystem auf das übrige System. Diese Kräfte heißen Oberflächenkräfte. Sie gehören zu den Kontaktkräften. In ihrer Stärke und Richtung sind sie abhängig von den vorher festgelegten Schnitten. Eine Oberflächenkraft ist also nur sinnvoll angegeben, wenn auch die zugehörige Oberfläche bzw. Schnittfläche angegeben wird.

Volumenkräfte sind Nichtkontaktkräfte. Wie beispielsweise die Gravitationskraft oder der Magnetismus greifen sie am ganzen Volumen an, d. h. auch im Innern eines freigeschnittenen Körpers. Auch ihre Stärke ist erst dann sinnvoll angegeben, wenn gleichzeitig das freigeschnittene Volumen, auf das die Kraft wirkt, angegeben wird. Befindet sich beispielsweise ein homogener Klotz in einem homogenen Schwerefeld (näherungsweise ein kleiner Klotz nahe der Erdoberfläche), so wirkt die Volumenkraft Fg{displaystyle F_{mathrm {g} }} auf ihn. Zerschneidet man diesen Klotz gedanklich in seiner Mitte, so wirkt dagegen auf jeden Teilklotz nur noch die Volumenkraft Fg/2{displaystyle F_{mathrm {g} }/2} (siehe dazu nebenstehende Abbildung).

Schwerelosigkeit im All und Schweben unter Wasser |

Beim Tauchen lässt sich ähnlich wie im Weltall ein Gefühl der Schwerelosigkeit erleben, wenn der Taucher sein Gewicht mit Ausgleichsgewichten an die Dichte des Wassers angepasst hat. Auf den Taucher wirkt, auch unter Wasser, die Schwerkraft als Volumenkraft. Das der Schwerelosigkeit ähnliche Gefühl stellt sich unter Wasser durch den Auftrieb ein – der hydrostatische Druck, der als Oberflächenkraft auf die Unterseite des Körpers wirkt, ist höher als der auf die Oberseite des Körpers wirkende Druck. Da nur die Volumenkraft, nicht aber die Oberflächenkraft auf das Gleichgewichtsorgan wirkt, kann man auch unter Wasser oben von unten unterscheiden.

Die Schwerelosigkeit im All, wo der Astronaut ebenfalls „ohne Gewicht“ ist, kann man betrachten als Zustand, wo (etwa durch den ständigen freien Fall der Raumstation auf der Kreisbewegung um die Erde herum) die Gewichtskraft in jedem Punkt des Körpers durch die Trägheitskraft kompensiert wird. In diesem Fall funktioniert das Gleichgewichtsorgan nicht (die Folge ist häufig die sogenannte Raumkrankheit), der Raumfahrer kann sich bei geschlossenen Augen nicht orientieren.

Kräfte mit nichtmechanischer Ursache |

Einige zur Zeit Newtons noch als verschieden angesehene Kräfte entpuppten sich als Ausdrucksformen von elektromagnetischen Kräften im Inneren von Materie. Diese Kräfte machen sich bemerkbar

• als elektromotorische Kraft, die Elektronen durch einen Leiter treibt,


• in der Kompressibilität und Viskosität von Fluiden,


• bei der Reibung zwischen den Oberflächen verschiedener Körper,


• beim Widerstand, den ein Körper einer Verformung entgegensetzt (Federkraft, Kompressibilität, Schubmodul).

Kraft und Determinismus |

Quadratische Abhängigkeit der Fallstrecke von der Fallzeit: Man sieht einen frei fallenden Ball im Licht von elf Stroboskopblitzen, die ihn im Abstand von je 0,05 Sekunden beleuchtet haben. Während der ersten 0,05 Sekunden durchfällt der Ball eine Längeneinheit (hier ungefähr 12 mm); innerhalb von 0,10 Sekunden vier Längeneinheiten; innerhalb von 0,15 Sekunden dann neun Längeneinheiten und so weiter, bis er nach 0,50 Sekunden hundert Längeneinheiten zurückgelegt hat.

Mit Hilfe der newtonschen Gesetze ist es möglich, aus einer gegebenen Ausgangssituation und den wirkenden Kräften die zeitliche Entwicklung eines physikalischen Systems vorherzusagen. Dies trifft nicht nur für einzelne Versuche im Labor zu, sondern im Prinzip auch auf das Universum als Ganzes. Diese Folgerung trug im 18. Jahrhundert zur Verbreitung eines deterministischen Weltbildes bei. Demnach wären alle Ereignisse grundsätzlich vorbestimmt, wenn auch die für eine Vorhersage erforderlichen Rechnungen in der Regel nicht praktisch durchführbar sind. Anfang des 20. Jahrhunderts stellte sich jedoch heraus, dass die Formeln der klassischen Physik auf der Ebene der Atome nicht anwendbar sind. Das aus den Formeln gefolgerte deterministische Weltbild musste daher in seiner ursprünglichen Form verworfen werden.^[22]

Zusammenhang von Kraft und Arbeit |

Durch das Wirken einer Kraft kann sich die Energie eines Körpers verändern. Ein Beispiel ist die Spannenergie beim Expander. Die beim Verschieben des Angriffspunktes einer Kraft um eine gewisse Wegstrecke übertragene Energie nennt man auch Arbeit und bezeichnet sie dann oft mit W{displaystyle W}.

Will man eine bestimmte Arbeit mit geringerer Kraft leisten, so ist dies mit einem Kraftwandler möglich. Beispiele für Kraftwandler sind Flaschenzüge, Hebel oder Gangschaltungen. Jedoch verlängert sich der Weg, längs dem die Kraft ausgeübt werden muss. Wird beispielsweise durch Verwendung eines Kraftwandlers nur ein Viertel der ohne ihn erforderlichen Kraft benötigt, so ist dies mindestens mit einer Vervierfachung des Weges verbunden. Diese Konsequenz des Energieerhaltungssatzes ist in der »Goldenen Regel der Mechanik« beschrieben.

Wenn die Kraft konstant ist und in Richtung eines geradlinigen Weges der Länge s{displaystyle s} wirkt, dann wird die aufzuwendende Arbeit durch die Beziehung

W=Fs{displaystyle W=F,s}

bestimmt. Falls die Kraft im Winkel α{displaystyle alpha } schräg zur Strecke wirkt, lässt sich die Arbeit durch folgende Formel berechnen:

W=F→⋅s→=|F→||s→|cos⁡α{displaystyle W={vec {F}}cdot {vec {s}}=|{vec {F}}|,|{vec {s}}|,cos alpha }

In obiger Gleichung ist s→{displaystyle {vec {s}}} der Vektor vom Startpunkt zum Endpunkt der Strecke. Insbesondere wird keine Arbeit geleistet, wenn die Kraft mit dem Weg einen rechten Winkel bildet: Das Tragen einer Last in der Ebene kann zwar mühsam sein, aber die Last nimmt dabei keine Energie auf.

Ganz allgemein ist die geleistete Arbeit das Kurvenintegral der Kraft entlang des zurückgelegten Wegs:

W=∫s→1s→2F→(s→)⋅ds→{displaystyle W=int _{{vec {s}}_{1}}^{{vec {s}}_{2}}{vec {F}}({vec {s}})cdot mathrm {d} {vec {s}}}

Dabei sind s→1{displaystyle {vec {s}}_{1}} und s→2{displaystyle {vec {s}}_{2}} die Ortsvektoren des Start- und des Endpunkts des Wegs.

Konservative und dissipative Kräfte |

Wird der Expander, um beim obigen Beispiel zu bleiben, einseitig fixiert und das andere Ende im Raum bewegt, so ändern sich von Punkt zu Punkt systematisch Richtung und Betrag der Kraft. Sofern die Bewegungen langsam ausgeführt werden, sodass keine Schwingungen des Expanders angeregt werden, und unter Vernachlässigung innerer Reibung, ist die Kraft lediglich eine Funktion des Ortes (ein statisches Vektorfeld). Dabei entspricht jedem Ort ein bestimmter Spannungszustand des Expanders. Es kommt nicht darauf an, auf welchem Weg der Ort und der zugehörige Spannungszustand erreicht wurde. In solchen Fällen spricht man von einer konservativen Kraft. Arbeit, die gegen eine konservative Kraft verrichtet wurde, ist vom Weg unabhängig, sie hängt nur vom Anfangs- und Endpunkt ab. Insbesondere erhält man verrichtete Arbeit zurück, wenn man – auf demselben oder einem anderen Weg – den Ausgangspunkt wieder erreicht.

Der Wert des Wegintegrals einer konservativen Kraft von einem festen Bezugspunkt aus heißt potentielle Energie Wpot{displaystyle W_{mathrm {pot} },}, meist auch Potential, zur Unterscheidung siehe aber Potentiale und Potentialfelder im Hauptartikel. Oft ist es einfacher, von der potentiellen Energie ausgehend (in obigem Beispiel also von der im Expander gespeicherten Spannenergie) die Kraft F→{displaystyle {vec {F}}} als ihren negativen Gradienten

F→(r→)=−∇Wpot(r→){displaystyle {vec {F}}({vec {r}})=-nabla W_{mathrm {pot} }({vec {r}})}

zu bestimmen, denn das Feld der potentiellen Energie ist nur ein Skalarfeld.

Dass an einem System geleistete Arbeit vollständig in potentielle Energie umgesetzt wird, ist in praktisch auftretenden Fällen nie erfüllt. Reibungskräfte müssen zusätzlich überwunden werden. Die gegen sie geleistete Arbeit wird in Wärme umgesetzt. Manchmal ist solche Dissipation erwünscht (Fallschirm, Fitnessgeräte, Motorbremse).

Kraft im Kraftfeld |

Gegen den Expander im obigen Beispiel muss das schmächtige Kerlchen dieselbe Kraft aufwenden wie der Schwergewichtler. In der Disziplin Treppensteigen arbeiten beide gegen ihre jeweilige Gewichtskraft FG{displaystyle F_{mathrm {G} }} und in der Erdumlaufbahn würden beide einträchtig nebeneinander schweben. Bei der Beschreibung von Bewegungen in Kraftfeldern, wie hier dem Erdschwerefeld, ist es oft nützlich, von jener Eigenschaft des Körpers, zu der die Kraft proportional ist, zu abstrahieren. Diese Eigenschaft (hier die Masse m{displaystyle m} des Sportlers) wird allgemein Ladung genannt. Die Abstraktion geschieht, indem das Vektorfeld der Kraft durch die Ladung geteilt wird. Das Resultat

F→G(r→)m=g→(r→){displaystyle {frac {{vec {F}}_{mathrm {G} }({vec {r}})}{m}}={vec {g}}({vec {r}})}

wird Feldstärke genannt und beschreibt das Kraftfeld unabhängig von der Ladung des Probekörpers. Die Feldstärke g des Schwerefeldes wird auch Fallbeschleunigung genannt.

Das für konservative Kraftfelder existierende Skalarfeld der potentiellen Energie geteilt durch die Ladung ergibt das Potential des Kraftfeldes.

Zusammenhang von Kraft und Drehmoment |

Hebelgesetz

Das Drehmoment M→{displaystyle {vec {M}}} kann als Drehwirkung der Kraft F→{displaystyle {vec {F}}} aufgefasst werden. Es ist das Kreuzprodukt von Kraftarm und Kraft:

M→=r→×F→{displaystyle {vec {M}}={vec {r}}times {vec {F}}}

Dabei ist der Kraftarm r→{displaystyle {vec {r}}} der Ortsvektor vom Drehpunkt zum Punkt, an dem die Kraft angreift (Angriffspunkt). Das bedeutet, je größer der Abstand zwischen Drehpunkt und Angriffspunkt ist, desto größer ist das Drehmoment. Außerdem trägt nur die Komponente der Kraft zum Drehmoment bei, die senkrecht zur Strecke zwischen Drehpunkt und Angriffspunkt ist.

Drehmomente treten unter anderem bei der Zu- oder Abnahme der Drehzahl von drehbaren Körpern auf. Sie spielen dabei eine vergleichbare Rolle wie Kräfte bei der geradlinigen Bewegung. Analog zum Kräftegleichgewicht ist das Drehmomentengleichgewicht ein wichtiger Spezialfall.

Zusammenhang von Kraft und Druck |

Wenn eine Kraft auf eine Fläche wirkt, so ist der dadurch erzeugte Druck p{displaystyle p} der Betrag (die Vektorlänge) der auf dieser Fläche senkrechtstehenden Kraftkomponente F→⊥{displaystyle {vec {F}}_{perp }} pro Flächeninhalt A{displaystyle A}:

p=|F→⊥|A{displaystyle p={frac {|{vec {F}}_{perp }|}{A}}}

Der Druck ist eine intensive Zustandsgröße thermodynamischer Systeme und zudem eine lineare Feldgröße. Dieses Konzept ist eine Vereinfachung des allgemeinen Spannungstensors.

Die Druckspannung ist im Gegensatz zum Druck keine skalare Zustandsgröße.

Trägheitskräfte bzw. Scheinkräfte |

Der Wechsel zwischen aristotelischer und newtonscher Auffassung der Kraft macht sich auch in der Bezeichnung „Scheinkraft“ (synonym dazu verwendet: Trägheitskraft) bemerkbar. Der Name „Scheinkraft“ kann irreführend sein; diese Kräfte sind durchaus messbar und rufen reale Wirkungen hervor. Die Bezeichnung rührt daher, dass sie nur in beschleunigten Koordinatensystemen auftreten und von einem Inertialsystem aus betrachtet nicht existieren. Ein geeigneter außenstehender Beobachter erklärt die Wirkungen einfach durch die Anwendung des Trägheitsprinzips ohne weitere Kräfte.

Ein anderer Zugang zum Begriff der Trägheitskraft ist mit dem d’Alembertschen Prinzip verbunden: Es wandelt – vereinfacht gesagt – das dynamische Problem des sich bewegenden Körpers durch die Einführung einer d’Alembertschen Trägheitskraft F→T=−ma→{displaystyle {vec {F}}_{T}=-m,{vec {a}}} in ein statisches Problem um. Die technische Mechanik, in der das Prinzip sehr erfolgreich angewendet wird, spricht von einem »dynamischen Gleichgewicht«. Während manche Fachbücher diese d’Alembertsche Trägheitskraft als Gegenkraft im Sinne des Wechselwirkungsprinzips bezeichnen,^[23] sehen andere Fachbuchautoren sie in Widerspruch zum Wechselwirkungsprinzip, da zu ihr keine Gegenkraft existiert.^[24][25] Die Bezeichnung Scheinkraft wird auch damit begründet, dass die Trägheitskraft der Definition von Newton, was unter einer wirkenden Kraft zu verstehen ist,^[26] nicht genüge.^[27]

• Wenn ein Auto durch eine Kraft F→{displaystyle {vec {F}}} abgebremst wird (Extremfall: Frontalaufprall), so wirkt diese Kraft nicht direkt auf den Fahrer. Gemäß dem Trägheitsprinzip wird sich der Fahrer also mit gleichbleibender Geschwindigkeit geradeaus bewegen, während das Auto sich verlangsamt. Erst durch die Rückhaltesysteme (Sicherheitsgurt und Airbag) werden Zwangskräfte auf den Fahrer ausgeübt, die ihn ebenfalls verlangsamen. Aus seiner Sicht wirkt nun eine nach vorn gerichtete Trägheitskraft, die ihn in Richtung der Windschutzscheibe befördert.


• Der Sitz eines Kettenkarussells würde sich ohne Kraftwirkung durch die Kette geradeaus fortbewegen, nur durch die zum Mittelpunkt der durchlaufenen Kreisbahn gerichtete Zentripetalkraft kommt die Kreisbewegung zustande. Ein Mensch auf dem Sitz verspürt die Zentrifugalkraft (Fliehkraft) als Trägheitskraft.

• Weitere Beispiele für Trägheitskräfte sind
  
  
  
  • die Corioliskraft
    
  
  
  • die Massenkräfte im Motorenbau
    
  
  
  • die Gravitation, betrachtet im Rahmen der allgemeinen Relativitätstheorie, siehe Gravitationskraft als Trägheitskraft
    
  
  
  
  

Kraft in der Relativitätstheorie |

Die spezielle Relativitätstheorie tritt an die Stelle der dynamischen Gesetze der klassischen Mechanik, wenn die betrachteten Geschwindigkeiten gegenüber der Lichtgeschwindigkeit nicht mehr vernachlässigbar sind. In der speziellen Relativitätstheorie muss der Impuls zum relativistischen Impuls verallgemeinert werden, die Kraft bleibt dann weiter aus F→=dp→dt{displaystyle {vec {F}}={tfrac {mathrm {d} {vec {p}}}{mathrm {d} t}}} berechenbar, aber der Impuls lässt sich nicht mehr durch die Beziehung p→=m⋅v→{displaystyle {vec {p}}=mcdot {vec {v}}} berechnen. An die Stelle der newtonschen Beziehung »Kraft = Masse mal Beschleunigung«, F→=m⋅a→{displaystyle {vec {F}}=mcdot {vec {a}}}, tritt die Gleichung

F→=ddtm⋅v→1−v2c2.{displaystyle {vec {F}}={frac {mathrm {d} }{mathrm {d} t}}{frac {mcdot {vec {v}}}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}.}

Die Kraft wird ferner zur Minkowskikraft („Viererkraft“) erweitert, die meist als Kμ{displaystyle K^{mu }} geschrieben wird und aus dem Viererimpuls berechnet werden kann über Kμ=dpμdτ=γdpμdt{displaystyle K^{mu }={tfrac {mathrm {d} p^{mu }}{mathrm {d} tau }}=gamma {tfrac {mathrm {d} p^{mu }}{mathrm {d} t}}} mit der Eigenzeit τ{displaystyle tau } und dem Lorentzfaktor

γ=11−v2c2.{displaystyle gamma ={frac {1}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}.}

Diese Gleichung, die »Bewegungsgleichung der speziellen Relativitätstheorie für den Viererimpuls«, beschreibt beschleunigte Bewegungen in einem Inertialsystem. Zwischen F→{displaystyle {vec {F}}} und K→{displaystyle {vec {K}}} besteht der Zusammenhang F→=1−v→2c2K→,{displaystyle {vec {F}}={sqrt {1-{frac {{vec {v}}^{2}}{c^{2}}}}},{vec {K}},} wobei K→=(K1,K2,K3){displaystyle {vec {K}}=(K^{1},K^{2},K^{3})} der räumliche Teil der Viererkraft Kμ{displaystyle K^{mu }} ist; der neu hinzukommende zeitliche Teil beschreibt eine Energieänderung, genauer: dEcdτ{displaystyle {tfrac {mathrm {d} {tfrac {E}{c}}}{mathrm {d} tau }}} (siehe Viererimpuls), sodass man auch vom Kraft-Leistung-Vierervektor spricht.

Die allgemeine Relativitätstheorie stellt eine Erweiterung der newtonschen Gravitationstheorie dar; sie enthält diese als Grenzfall für hinreichend kleine Massendichten und Geschwindigkeiten. Ihre Grundlagen wurden maßgeblich von Albert Einstein zu Beginn des 20. Jahrhunderts entwickelt, sie beschreibt allgemein die Wechselwirkung zwischen Materie (einschließlich Feldern) einerseits und Raum und Zeit andererseits.

Die Gravitationskraft wird in der allgemeinen Relativitätstheorie als geometrische Eigenschaft der gekrümmten vierdimensionalen Raumzeit verstanden: Energie, Impuls und Druck der Materie beeinflussen die Geometrie der Raumzeit, in der sie sich befinden. Dieser Einfluss lässt sich durch den Begriff der »Raumzeitkrümmung« beschreiben. Die räumlichen und zeitlichen Koordinaten werden als gleichberechtigt betrachtet, alle Änderungen werden nur mehr als geometrisches Problem behandelt. Materie, auf die eine Gravitationskraft ausgeübt wird, bewegt sich in der Raumzeit entlang einer Geodäte, also so, wie es im naiven Sinn mit »geradeaus« gemeint ist. Die Gerade als Modell für die Geradeausbewegung des freien Körpers gibt es nur in ungekrümmten (also gravitationsfreien) Räumen.

Physikalisch entspricht die Bewegung entlang einer Geodäte dem freien Fall. Ein Großteil der Schwerkraft wird somit darauf zurückgeführt, dass der Erdboden durch die gegenseitige Abstoßung der Atome, aus denen die Erde besteht, relativ zu einem frei fallenden Gegenstand nach oben beschleunigt wird. Das entspricht in etwa der Erfahrung beim Abbremsen eines nach unten fahrenden Fahrstuhls. Abgesehen von Gezeitenkräften verspürt ein Mensch auf dem Erdboden also fast die gleiche Kraft, als würde er in einer gleichmäßig beschleunigten Rakete stehen. Diese Gezeitenkräfte, die in jedem Gravitationsfeld herrschen, zeigen sich bei einem ausgedehnten Objekt als Verformungskräfte. Im Gravitationsfeld eines kugelförmigen Körpers (wie der Erde) ziehen die Gezeitenkräfte das Objekt in Fallrichtung in die Länge und schieben es senkrecht zur Fallrichtung zusammen. Gezeitenkräfte folgen direkt aus der Raumzeitkrümmung und sind besonders stark bei sehr massereichen Objekten wie einem Schwarzen Loch.^[28]

Kraft in der Quantenmechanik |

Bei der Wechselwirkung kleinster Teilchen liefern Experimente Ergebnisse, die der klassischen Mechanik widersprechen. Insbesondere sind bestimmte Größen quantisiert, das heißt, sie treten nur in bestimmten Portionen auf – den sogenannten »Quanten«. Während die Kraft selbst nicht quantisiert ist, können Kräfte eine Quantelung der möglichen Teilchenenergien bewirken.

In der Quantenmechanik werden in der Regel Kräfte nicht explizit betrachtet. Die von Kräften verursachten Phänomene werden – analog zur klassischen Mechanik – durch das Potential beschrieben.

Es gibt quantenmechanische Effekte, die sich wie eine Kraft bemerkbar machen, aber nicht auf eine der Grundkräfte zurückzuführen sind. Beispiele sind das Pauli-Prinzip und die Austauschwechselwirkung.

Kraft in den Quantenfeldtheorien |

Ab 1927 wurde versucht, die „Quantisierung“ nicht nur auf die ursprünglichen Objekte der Quantenmechanik, die Partikel, sondern auch auf Felder (z. B. das elektrische Feld) anzuwenden, woraus die Quantenfeldtheorien entstanden; man spricht auch von der »zweiten Quantisierung«. Die Quantisierung der Felder wird auch im Bereich der Festkörperphysik und in anderen Vielteilchentheorien angewandt.

In der Quantenfeldtheorie werden alle Kräfte auf den Austausch von virtuellen Bosonen zurückgeführt, diese Wechselwirkungsteilchen zu jeder Grundkraft sind sozusagen einzelne »Kraftteilchen« oder auch »Kraftträger«.

Konkrete Quantenfeldtheorien sind die Quantenelektrodynamik (diese beschreibt Elektronen, Positronen und das elektromagnetische Feld) und die Quantenchromodynamik (diese beschreibt die starke Kernkraft, also unter anderem den inneren Aufbau der Protonen und Neutronen). Außerdem wurde die schwache Kernkraft mit der Quantenelektrodynamik zur Theorie der elektroschwachen Wechselwirkung zusammengeführt. Das elektroschwache Modell bildet mit der Quantenchromodynamik das sogenannte Standardmodell der Elementarteilchenphysik. Es enthält alle bekannten Teilchen und kann die meisten bekannten Vorgänge erklären. Im Standardmodell fungieren Eichbosonen als Kraftteilchen zur Vermittlung von Wechselwirkungen, die Gravitationskraft ist jedoch nicht enthalten. Auch hier werden solche Wechselwirkungsteilchen angenommen, genannt Gravitonen.

Vereinheitlichung der Grundkräfte |

Kopplungskonstanten α als Funktion der Energie E (starke, schwache, elektromagnetische Wechselwirkung, Gravitation)

In der heutigen Physik werden meist vier Grundkräfte bzw. Wechselwirkungen unterschieden. Sortiert nach zunehmender relativer Stärke – als Maß dafür dient üblicherweise die Kopplungskonstante – sind das:

• Gravitationskraft


• Schwache Kernkraft


• Elektromagnetische Kraft


• Starke Kernkraft

Eines der Ziele der Physik ist es, in einer »großen vereinheitlichten Theorie« alle Grundkräfte oder Wechselwirkungen in einem vereinheitlichten Gesamtkonzept zu beschreiben, wie in der Tabelle dargestellt. Dazu nimmt man an, dass diese Grundkräfte zum Zeitpunkt des Urknalls eine einzige Kraft waren, die sich infolge der Abkühlung in die einzelnen Kräfte aufspaltete.

Auf diesem Weg gab es bereits Erfolge, zunächst bei der Zusammenfassung der elektrischen Wechselwirkung und der magnetischen Wechselwirkung zur elektromagnetischen Wechselwirkung durch die Elektrodynamik von James Clerk Maxwell. Die Wechselwirkungen zwischen elektrischen und magnetischen Feldern lassen sich auf andere Weise auch relativistisch erklären.

Ebenso ist es bereits gelungen, die elektromagnetische Wechselwirkung und die schwache Wechselwirkung in der Quantenfeldtheorie der elektroschwachen Wechselwirkung vereinheitlicht zu beschreiben.

Statische Kraft und dynamische Kraft |

In der Technischen Mechanik unterscheidet man zwischen statischen^[29] und dynamischen (bzw. harmonischen^[29][30]) Kräften. Statische Kräfte sind diejenigen, die zeitlich unverändert wirken, dynamische Kräfte sind zeitlich veränderliche Kräfte. Bei sehr langsamer zeitlicher Veränderung spricht man von quasistatischen Kräften.

In Biomechanik und Sportmedizin ist die statische Kraft diejenige Kraft, die ein Muskel oder eine Muskelgruppe willkürlich gegen einen fixierten Widerstand ausüben kann.^[31][32] Die dynamische Kraft „ist die willkürlich ausgeübte Bewegung einer Masse innerhalb eines programmierten Vorgangs“,^[32] ein Beispiel ist die Schnellkraft.

Literatur |

• Wolfgang Nolting: Klassische Mechanik. In: Grundkurs Theoretische Physik. Bd. 1, 8. Auflage. Springer, Berlin 2008, ISBN 978-3-540-34832-0.


• Richard P. Feynman: Feynman-Vorlesungen über Physik. Mechanik, Strahlung, Wärme. 5., verbesserte Auflage, definitive Edition. Oldenbourg, München / Wien 2007, ISBN 978-3-486-58444-8 (= The Feynman Lectures on Physics. Band 1).


• Paul A. Tipler: Physik. 3. korrigierter Nachdruck der 1. Auflage. 1994, Spektrum Akademischer Verlag, Heidelberg / Berlin 2000, ISBN 3-86025-122-8.


• Ludwig Bergmann, Clemens Schaefer: Mechanik – Akustik – Wärme. In: Lehrbuch der Experimentalphysik. Bd. 1, 12. Auflage. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-019311-4.


• 
  Max Jammer: Concepts of Force: A Study in the Foundations of Dynamics. Cambridge (Mass): Harvard U.P., 1957 New York: Harper, 1962 New York: Dover, 1999. ISBN 0-486-40689-X.

Weblinks |

 Wikiquote: Kraft – Zitate

 Wiktionary: Kraft – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• 
  Kraftmessung mit Hilfe des Gesetzes von Hooke. LEIFI, auf Schülerniveau.


• 
  Flash-Animation zur Kräfteaddition. dwu-Unterrichtsmaterialien, auf Schülerniveau.


• Cornelis Harm Glimmerveen: The force of dialectics: on the logical and ontological structures concerning the concepts of force in Leibniz, Kant, and Hegel. Diss. Groningen 1992 (zum Kraftbegriff bei Leibniz, Kant und Hegel).

Einzelnachweise und Fußnoten |

1. 
   ↑ Ludwig Bergmann, Clemens Schaefer u. a.: Lehrbuch der Experimentalphysik, Bd. 1. Mechanik, Relativität, Wärme. 11. Auflage. de Gruyter, 1998, ISBN 978-3-11-012870-3. , Abschnitt 4.1 Masse und Kraft.
   


2. 
   ↑ Richard P. Feynman, Robert B. Leighton, Matthew Sands: Mechanik. Walter de Gruyter GmbH & Co KG, Berlin/Boston 2015, ISBN 978-3-11-044460-5, S. 133 (Google Books). 
   


3. 
   ↑ Günther Drosdowski, Paul Grebe: Das Herkunftswörterbuch. Die Etymologie der deutschen Sprache. Bd. 7. Dudenverlag, Mannheim 1963, ISBN 978-3-411-00907-7, S. 364. 
   


4. 
   ↑ ^abc Wolfgang Pfeifer (Leitung): Etymologisches Wörterbuch des Deutschen. Ungekürzte, durchgesehene Ausgabe. Deutscher Taschenbuch Verlag, München 1995. ISBN 3-05-000626-9; 7. Aufl. 2004, ISBN 3-423-32511-9. Eine digitale Fassung dieses Wörterbuchs ist im lexikalischen Informationssystem abrufbar: dwds.de.
   


5. 
   ↑ Philosophiae Naturalis Principia Mathematica. 1687, deutsche Ausgabe Mathematische Prinzipien der Naturlehre. Übersetzt und erläutert von Jacob Philip Wolfers, Oppenheim, Berlin 1872. (Unveränderter Nachdruck Minerva, 1992, ISBN 3-8102-0939-2).
   


6. 
   ↑ Moritz Rühlmann: Vorträge über die Geschichte der technischen Mechanik und theoretischen Maschinenlehre und der damit im Zusammenhang stehenden mathematischen Wissenschaften. Baumgärtner, Leipzig 1885.  Nachdruck: Documenta technica, Reihe 1, Darstellungen zur Technikgeschichte, Verlag Olms, Hildesheim 1979.
   


7. 
   ↑ Hans Peter Sang: Geschichte der Physik. Klett, Stuttgart 1999, ISBN 3-12-770230-2, S. 7. 
   


8. 
   ↑ Károly Simonyi: Kulturgeschichte der Physik. Harri Deutsch, Thun, Frankfurt a. M. 1995, ISBN 3-8171-1379-X, S. 77. 
   


9. 
   ↑ Richard S. Westfall: Force in Newton’s Physics: The Science of Dynamics in the Seventeenth Century. American Elsevier, New York 1971. 
   


10. 
    ↑ ^ab Károly Simonyi: Kulturgeschichte der Physik. Harri Deutsch, Thun, Frankfurt a. M. 1995, ISBN 3-8171-1379-X. 
    


11. 
    ↑ Friedrich Albert Carl Gren: Grundriss der Naturlehre. 3. Auflage. Hemmerde & Schwetschke, Halle 1797.  S. 1 ff: „§ 1: Natur heißt der Inbegriff der Kräfte eines Dinges. § 2: Kraft nennen wir jede Ursache der Veränderung des Zustands eines Dinges oder der Dinge. § 3:(…) Kraft ist, was Bewegung hervorbringt oder hemmt.“
    


12. 
    ↑ Gunter Lind: Physik im Lehrbuch 1700–1850. Springer, Berlin 1992, ISBN 3-540-55138-7. 
    


13. 
    ↑ Erhard Scheibe: Die Philosophie der Physiker. 2. Auflage. C.H.Beck, München 2012, S. 22 ff. 
    


14. 
    ↑ Hegel beklagt (Enzyklopädie der philosophischen Wissenschaften im Grundrisse. § 270): „… die Überschwemmung der physischen Mechanik mit einer unsäglichen Metaphysik, die – gegen Erfahrung und Begriff – jene mathematischen Bestimmungen allein zu ihrer Quelle hat.“ Siehe auch: Enzyklopädie der philosophischen Wissenschaften im Grundrisse. § 137.
    


15. 
    ↑ Andreas Kleinert: Aufklärung durch Physik. In: Walter Schmitz/Carsten Zelle (Hrsg.): Innovation und Transfer. Eckard Richter, Dresden 2004, ISBN 3-933592-37-2, S. 11–20.  Wenn Fernwirkungen möglich seien, so Euler, dann müsse man befürchten, Verdauungsprobleme von den Kräutern zu bekommen, die auf dem Saturn wachsen, auch ohne sie gegessen zu haben.
    


16. 
    ↑ In diesem Zusammenhang wurde zeitweise nicht die Masse, sondern die Kraft als Grundgröße benutzt und die jeweils andere Größe als „abgeleitete Größe“ bezeichnet: Man verwendete damals als Grundgröße die Krafteinheit „1 Kilopond“ statt der vorher und nachher üblichen Masseneinheit „1 Kilogramm“, indem man für die entsprechenden Gewichtskräfte per Gesetz Messverfahren zur Eichung vorschrieb.
    


17. 
    ↑ Christian Meier: Grenzflächenphysik. Kleinster Abschleppdienst der Welt. Auf: wissenschaft-online.de. 21. Februar 2008, abgerufen am 2. März 2015.
    


18. 
    ↑ S. Knünz, M. Herrmann, V. Batteiger, G. Saathoff, T. W. Hänsch, K. Vahala, Th. Udem: Injection locking of a trapped-ion phonon laser. In: Physical Review Letters. 105, 2010, 013004.
    


19. 
    ↑ International Bureau of Weights and Measures (Hrsg.): The international system of units. U.S. Dept. of Commerce, National Bureau of Standards, 1977, ISBN 0-7456-4974-2, S. 17 (englisch, eingeschränkte Vorschau in der Google-Buchsuche). 
    


20. 
    ↑ H. Schrecker: Der Weg zum physikalischen Kraftbegriff von Aristoteles bis Newton. In: Naturwissenschaften im Unterricht Physik/Chemie. 36, Nr. 34, 1988. Gekürzte Fassung. (Memento vom 20. Januar 2012 im Internet Archive).
    


21. 
    ↑ ^abc H. Egerer: Ingenieur-Mechanik. Lehrbuch der technischen Mechanik in vorwiegend graphischer Behandlung. Band 1. Springer, Berlin, Heidelberg 1919, ISBN 978-3-662-32061-7, S. 124 (google.de [abgerufen am 3. Januar 2017]). 
    


22. 
    ↑ Carl Hoefer: Causal Determinism. Artikel in der Stanford Encyclopedia of Philosophy (englisch).
    


23. 
    ↑ Hans J. Paus: Physik in Experimenten und Beispielen. S. 33, eingeschränkte Vorschau in der Google-Buchsuche.
    


24. 
    ↑ Dietmar Gross, Werner Hauger, Jarg Schrader, Wolfgang A. Wall: Technische Mechanik: Band 3: Kinetik. 10. Auflage. Gabler Wissenschaftsverlage, 2008, S. 191 (eingeschränkte Vorschau in der Google-Buchsuche – „Wir schreiben nun und fassen das negative Produkt aus der Masse m und der Beschleunigung a formal als eine Kraft auf, die wir […] D’alembertsche Trägheitskraft F_T nennen: F_T=−ma. Diese Kraft ist keine Kraft im Newtonschen Sinne, da zu ihr keine Gegenkraft existiert (sie verletzt das Axiom actio=reactio!); wir bezeichnen sie daher als Scheinkraft.“). 
    


25. 
    ↑ Rolf Isermann: Mechatronische Systeme: Grundlagen. 2. Auflage. Gabler Wissenschaftsverlage, 2004, ISBN 3-540-32336-8, S. 124 (eingeschränkte Vorschau in der Google-Buchsuche). 
    


26. 
    ↑ Bruno Assmann, Peter Selke: Technische Mechanik Band 3: Kinematik und Kinetik. 15. Auflage. Oldenbourg Verlag, 2010, ISBN 3-486-59751-5, S. 246 (eingeschränkte Vorschau in der Google-Buchsuche – „Newton hat als erster versucht, die Physik systematisch aufzubauen. An den Anfang seines (…) Hauptwerkes (…) stellt er vier Definitionen: (…) Definition 4: Eine wirkende Kraft ist das gegen einen Körper ausgeübte Bestreben, seinen Bewegungszustand zu ändern, entweder den der Ruhe oder den der gleichförmigen geradlinigen Bewegung.“). 
    


27. 
    ↑ Bruno Assmann, Peter Selke: Technische Mechanik Band 3: Kinematik und Kinetik. 15. Auflage. Oldenbourg Verlag, 2010, ISBN 3-486-59751-5, S. 246 (eingeschränkte Vorschau in der Google-Buchsuche). 
    


28. 
    ↑ Norbert Dragon: Geometrie der Relativitätstheorie. (Memento des Originals vom 19. April 2009 im Internet Archive)  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.itp.uni-hannover.de Vorlesungsskript (PDF; 2,4 MB), abgerufen am 15. Juli 2014.
    


29. 
    ↑ ^ab Jürgen Grabe, Klaus-Peter Mahutka: Finite-Elemente-Analyse zur Vibrationsrammung von Pfählen. In: Bautechnik. Band 82, Nr. 9. Wiley Online Library, 2005, S. 632–640, doi:10.1002/bate.200590192. 
    


30. 
    ↑ Markus Waltering, Danièle Waldmann, Stefan Maas, Arno Zürbes: Untersuchung nichtlinearer Schwingungseigenschaften zur zerstörungsfreien Zustandsprüfung am Beispiel von Stahlbetonbalken. In: Beton- und Stahlbetonbau. Band 102, Nr. 9. Wiley Online Library, 2007, S. 615–621, doi:10.1002/best.200700572. 
    


31. 
    ↑ Wildor Hollmann, Heiko K. Strüder: Sportmedizin. Grundlagen für körperliche Aktivität, Training und Präventivmedizin. 5. Auflage. Schattauer Verlag, 2009, ISBN 978-3-7945-2546-1 (google.at). 
    


32. 
    ↑ ^ab Freerk T. Baumann: 6 Krafttraining mit Krebspatienten. In: Bewegungstherapie und Sport bei Krebs. Leitfaden für die Praxis; mit 22 Tabellen. Deutscher Ärzteverlag, 2008, ISBN 978-3-7691-0564-3, S. 57 f. (274 S., eingeschränkte Vorschau in der Google-Buchsuche). 
    

Dieser Artikel wurde am 11. August 2009 in dieser Version in die Liste der lesenswerten Artikel aufgenommen.