Ytukyg

Verschiedene Auffassungen von Polygonen und polygonalen Flächen

Ein Polygon (von altgriechisch πολυγώνιον polygṓnion ‚Vieleck‘; aus πολύς polýs ‚viel‘ und γωνία gōnía ‚Winkel‘)^[1] oder auch Vieleck ist in der elementaren Geometrie eine ebene geometrische Figur, die durch einen geschlossenen Streckenzug gebildet und/oder begrenzt wird, beziehungsweise ein zweidimensionales Polytop.

Ein Polygon erhält man, indem in einer Zeichenebene mindestens drei verschiedene (nicht kollineare) Punkte miteinander verbunden werden durch Strecken, Kanten oder Seiten genannt, sodass ein geschlossener Polygonzug mit ebensovielen Ecken entsteht, beispielsweise ein Dreieck oder ein Viereck. Die umschlossene Fläche wird unterschiedlich aufgefasst oft auch als Polygon bezeichnet, so in der Planimetrie.

Definition und Bezeichnungen |

Ein Polygon ist eine Figur, die durch ein Tupel
P:=(P1,P2,…,Pn),Pi∈R2,1≤i≤n{displaystyle P:=left(P_{1},P_{2},dotsc ,P_{n}right),P_{i}in mathbb {R} ^{2},1leq ileq n}
von n{displaystyle n} verschiedenen Punkten definiert ist.

• Die n{displaystyle n} Punkte heißen die Eckpunkte oder kurz Ecken des Polygons, ein Polygon mit n{displaystyle n} Ecken heißt n{displaystyle n}-Eck oder (insbesondere in der englischen Literatur) auch n{displaystyle n}-Gon.
  


• Die Strecken PiPi+1¯(i=1,…,n−1){displaystyle {overline {P_{i}P_{i+1}}}left(i=1,dotsc ,n-1right)} und PnP1¯{displaystyle {overline {P_{n}P_{1}}}} bezeichnet man als Seiten des Polygons.


• Alle Verbindungsstrecken zweier Eckpunkte, die keine Seiten sind, nennt man Diagonalen.

Manchmal werden noch weitere Bedingungen für die Definition eines Polygons vorausgesetzt, die aber formal nicht notwendig sind:

• Ein Polygon hat mindestens drei paarweise voneinander verschiedene Eckpunkte. Das schließt ein „Zweieck“ aus.


• Drei angrenzende Eckpunkte liegen nicht auf einer Geraden. Auch Pn{displaystyle P_{n}}, P1{displaystyle P_{1}}, P2{displaystyle P_{2}} und Pn−1{displaystyle P_{n-1}}, Pn{displaystyle P_{n}}, P1{displaystyle P_{1}} gelten dabei als angrenzende Eckpunkte. Das schließt Ecken mit gestrecktem Winkel aus.

Klassifikation |

Historische Abbildung von Vielecken (1699)

Nach Anzahl der Ecken |

Polygone werden typischerweise nach der Zahl der Ecken (Wertigkeit des Polygons) benannt:

• 
  Eineck (Monogon)


• 
  Zweieck (Digon)


• 
  Dreieck (Trigon)


• 
  Viereck (Tetragon)


• 
  Fünfeck (Pentagon)


• 
  Sechseck (Hexagon)


• 
  Siebeneck (Heptagon)


• 
  Achteck (Oktogon, aber englisch octagon)


• 
  Neuneck (Nonagon)


• 
  Zehneck (Dekagon)


• 
  Elfeck (Hendekagon)


• 
  Zwölfeck (Dodekagon)


• 
  Dreizehneck (Tridekagon)


• 
  Vierzehneck (Tetradekagon)


• 
  Fünfzehneck (Pentadekagon)


• 
  Sechzehneck (Hexadekagon)


• 
  Siebzehneck (Heptadekagon)


• 
  Achtzehneck (Oktodekagon)


• 
  Neunzehneck (Nonadekagon, englisch auch enneadecagon, enneakaidecagon)


• 
  Zwanzigeck (Ikosagon)


• 
  Einundzwanzigeck (Ikosihenagon)


• 
  Dreißigeck (Triacontagon)


• 
  Vierzigeck (Tetracontagon)


• 
  51-Eck (Pentakontahenagon)


• 
  Hunderteck (Hektogon)


• 257-Eck


• 
  Tausendeck (Chiliagon)


• 
  Zehntausendeck (Myriagon)


• 65537-Eck


• 
  1000000-Eck (Megagon)


• 4294967295-Eck


• 
  Googolgon (Googoleck)

Weitere Typen |

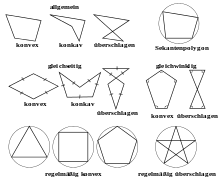
Klassifikation von Polygonen

• Schneiden (berühren) sich die Kanten nicht nur in den Eckpunkten, bezeichnet man das Polygon als überschlagen. Liegt keine Selbstüberschneidung vor, bezeichnet man das Polygon als einfach.


• Nicht überschlagene Vielecke können konvex (alle Innenwinkel sind kleiner als 180°) oder nichtkonvex (mindestens ein Innenwinkel ist größer als 180°) sein.


• Man unterscheidet in der Ebene liegende (planare) und im Raum liegende (nicht-planare) Polygone.


• Polygone können gleichseitig oder gleichwinklig sein. Hat ein Polygon sowohl gleiche Seiten, als auch gleiche Innenwinkel, dann wird es als regelmäßiges Polygon oder reguläres Polygon bezeichnet.


• Planare überschlagene reguläre Polygone werden wegen ihres Aussehens auch als Sternpolygone bezeichnet.


• Bei orthogonalen Polygonen treffen alle Kanten im rechten Winkel aufeinander (das heißt, der Innenwinkel beträgt an jeder Kante entweder 90° oder 270°).

Eigenschaften |

Winkel |

In einem nicht überschlagenen, ebenen n{displaystyle n}-Eck ist die Summe der Innenwinkel

α1+⋯+αn=(n−2)⋅180∘{displaystyle alpha _{1}+dotsb +alpha _{n}=(n-2)cdot 180^{circ }}.

Für die Summe der Außenwinkel gilt dann unabhängig von der Zahl der Ecken

α1′+⋯+αn′=360∘{displaystyle alpha _{1}'+dotsb +alpha _{n}'=360^{circ }}.

Sind darüber hinaus alle Innen- und Außenwinkel gleich groß, so haben diese den Wert

α=(n−2)n⋅180∘{displaystyle alpha ={frac {(n-2)}{n}}cdot 180^{circ }}   bzw.   α′=1n⋅360∘{displaystyle alpha '={frac {1}{n}}cdot 360^{circ }}.

Diagonalen |

Für nicht überschlagene Polygone gilt zur Berechnung der Anzahl der Diagonalen folgende Überlegung:

1. Jede der n{displaystyle n} Ecken kann durch eine Strecke mit einer der anderen Ecken verbunden werden.


2. Die Verbindung von Ecke Pa{displaystyle P_{a}} zur Ecke Pb{displaystyle P_{b}} ist mit der Verbindung von Pb{displaystyle P_{b}} nach Pa{displaystyle P_{a}} identisch.


3. Genau n{displaystyle n} Verbindungen sind Seiten des Polygons.

Also hat ein nicht überschlagenes n{displaystyle n}-Eck genau n⋅(n−1)2−n=n⋅(n−3)2{displaystyle {tfrac {ncdot (n-1)}{2}}-n={tfrac {ncdot (n-3)}{2}}} Diagonalen. Bei einem nichtkonvexen Polygon gibt es (im Bereich eines überstumpfen Innenwinkels) Diagonalen außerhalb des Polygons.

Umfang |

Wenn die Eckpunkte eines ebenen einfachen Polygons durch kartesische Koordinaten (xi,yi){displaystyle (x_{i},y_{i})} gegeben sind, kann der Umfang des Polygons durch Addition der mit dem Satz des Pythagoras berechneten Seitenlängen bestimmt werden:

U = (x1−xn)2+(y1−yn)2 + ∑i=1n−1(xi+1−xi)2+(yi+1−yi)2{displaystyle mathrm {U} = {sqrt {(x_{1}-x_{n})^{2}+(y_{1}-y_{n})^{2}}} + sum _{i=1}^{n-1}{sqrt {(x_{i+1}-x_{i})^{2}+(y_{i+1}-y_{i})^{2}}}}

Fläche |

Wenn die Eckpunkte eines ebenen einfachen Polygons durch kartesische Koordinaten (xi,yi){displaystyle (x_{i},y_{i})} gegeben sind, kann die Fläche des Polygons nach der gaußschen Trapezformel berechnet werden:

2A = |∑i=1n(yi+yi+1)⋅(xi−xi+1)| = |∑i=1n(xi+xi+1)⋅(yi+1−yi)| = |∑i=1n(xi⋅yi+1−yi⋅xi+1)|{displaystyle mathrm {2} A = left|sum _{i=1}^{n}(y_{i}+y_{i+1})cdot (x_{i}-x_{i+1})right| = left|sum _{i=1}^{n}(x_{i}+x_{i+1})cdot (y_{i+1}-y_{i})right| = left|sum _{i=1}^{n}(x_{i}cdot y_{i+1}-y_{i}cdot x_{i+1})right|}.

Hierbei werden die Indizes, die größer als n{displaystyle n} sind, immer modulo n{displaystyle n} betrachtet, das heißt mit xn+1{displaystyle x_{n+1}} ist x1{displaystyle x_{1}} gemeint:

2A = |xn⋅y1−yn⋅x1+∑i=1n−1(xi⋅yi+1−yi⋅xi+1)|{displaystyle 2A = left|x_{n}cdot y_{1}-y_{n}cdot x_{1}+sum _{i=1}^{n-1}(x_{i}cdot y_{i+1}-y_{i}cdot x_{i+1})right|}

In Determinantenform lautet die gaußsche Trapezformel:

2A = ||xnynx1y1|+∑i=1n−1|xiyixi+1yi+1||{displaystyle 2A = left|quad {begin{vmatrix}x_{n}&y_{n}\x_{1}&y_{1}end{vmatrix}}+sum _{i=1}^{n-1}{begin{vmatrix}x_{i}&y_{i}\x_{i+1}&y_{i+1}end{vmatrix}}quad right|}

Neben der gaußschen Trapezformel kann die Fläche eines Polygons durch eine vorzeichenbehaftete Summe der Flächeninhalte von Dreiecken berechnet werden, die mit den Kanten des Polygons als Basen und einem festen Punkt (zum Beispiel dem Ursprungspunkt) als Spitze gebildet werden. Die Flächeninhalte der Dreiecke mit einer dem festen Punkt abgewandten Basis (als Kante des Polygons) werden dabei mit negativen Vorzeichen versehen.^[2]

Der Flächeninhalt von Gitterpolygonen, deren Ecken alle auf einem Gitter liegen, kann mit dem Satz von Pick berechnet werden.

Verwendung |

In der Informatik sind wichtige Approximationen komplexer Polygone die konvexe Hülle und das minimal umgebende Rechteck. In Algorithmen wird oft erst anhand der Approximation auf einen möglichen nichtleeren Schnitt mit einem anderen geometrischen Objekt getestet (oder dieser ausgeschlossen), erst anschließend das ganze Polygon in den Speicher geladen und ein exakter Schnitt berechnet.

In der 3D-Computergrafik werden neben anderen Verfahren der geometrischen Modellierung beliebige (auch gekrümmte) Oberflächen als Polygonnetz modelliert. Dreiecksnetze eignen sich besonders gut zur schnellen Darstellung von Oberflächen, können allerdings nicht so gut durch Subdivision Surfaces interpoliert werden. Zur Speicherung von polygonalen Netzen gibt es eine Reihe bekannter Datenstrukturen.

Siehe auch |

• Konstruierbares Polygon


• Polyeder

Weblinks |

 Commons: Polygon – Sammlung von Bildern, Videos und Audiodateien

 Wiktionary: Polygon – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Wiktionary: Vieleck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• 
  Eric W. Weisstein: Polygon. In: MathWorld (englisch).


• Zur Mathematik unregelmäßiger Polygone


• Online-Berechnung von ebenen Polygonen mit graphischer Ausgabe

Einzelnachweise |

1. 
   ↑ Wilhelm Gemoll: Griechisch-Deutsches Schul- und Handwörterbuch. G. Freytag Verlag/Hölder-Pichler-Tempsky, München/Wien 1965. 
   


2. 
   ↑ [1] (PDF; 66 kB), Zhang, Cha, and Tsuhan Chen. "Efficient feature extraction for 2D/3D objects in mesh representation." Image Processing, 2001. Proceedings. 2001 International Conference on. Vol. 3. IEEE, 2001. APA.